微专题15 指数函数及其性质（解析版）.docx

《微专题15 指数函数及其性质（解析版）.docx》由会员分享，可在线阅读，更多相关《微专题15 指数函数及其性质（解析版）.docx（31页珍藏版）》请在第壹文秘上搜索。

1、微专题15指数函数及其性质【方法技巧与总结】知识点一、指数函数的图象及性质:y=ax0vl时图象图象IZ(o,i)Z-2二刊o?A-定义域R,值域(0,+)性质=l,即X=O时，y=l,图象都经过(0,1)点优=。，即=l时，)，等于底数。在定义域上是单调减函数在定义域上是单调增函数XVO时，axx0f,0优1XVO时，0at0时，axI既不是奇函数，也不是偶函数知识点诠释：(1)当底数大小不定时，必须分和“Ovavl”两种情形讨论.(2)当OVaVl时，x+oo,y-0;当白l时x-co,y0.当l时，的值越大，图象越靠近y轴，递增速度越快.当0vl时，。的值越小，图象越靠近y轴，递减的速度

2、越快.(3)指数函数)，=与y=的图象关于y轴对称.知识点二、指数函数底数变化与图像分布规律y=，y=bx,y=c,y=,则：Obad)时，bxaxdxaxdxcx(2)特殊函数【题型归纳目录】题型一：指数函数的图象基本性质：定点、对称性、单调性题型二：指数(型)函数的单调性应用(1):复合函数的值域问题题型三：指数(型)函数的单调性应用(2):复合函数的单调问题题型四：指数(型)函数中的奇偶性及与单调性的综合【典型例题】题型一：指数函数的图象基本性质：定点、对称性、单调性例1.已知函数/(力=少-4的图象关于直线x=2对称，则=()A.1B.2C.0D.-2【答案】B【解析】函数)，=2N的

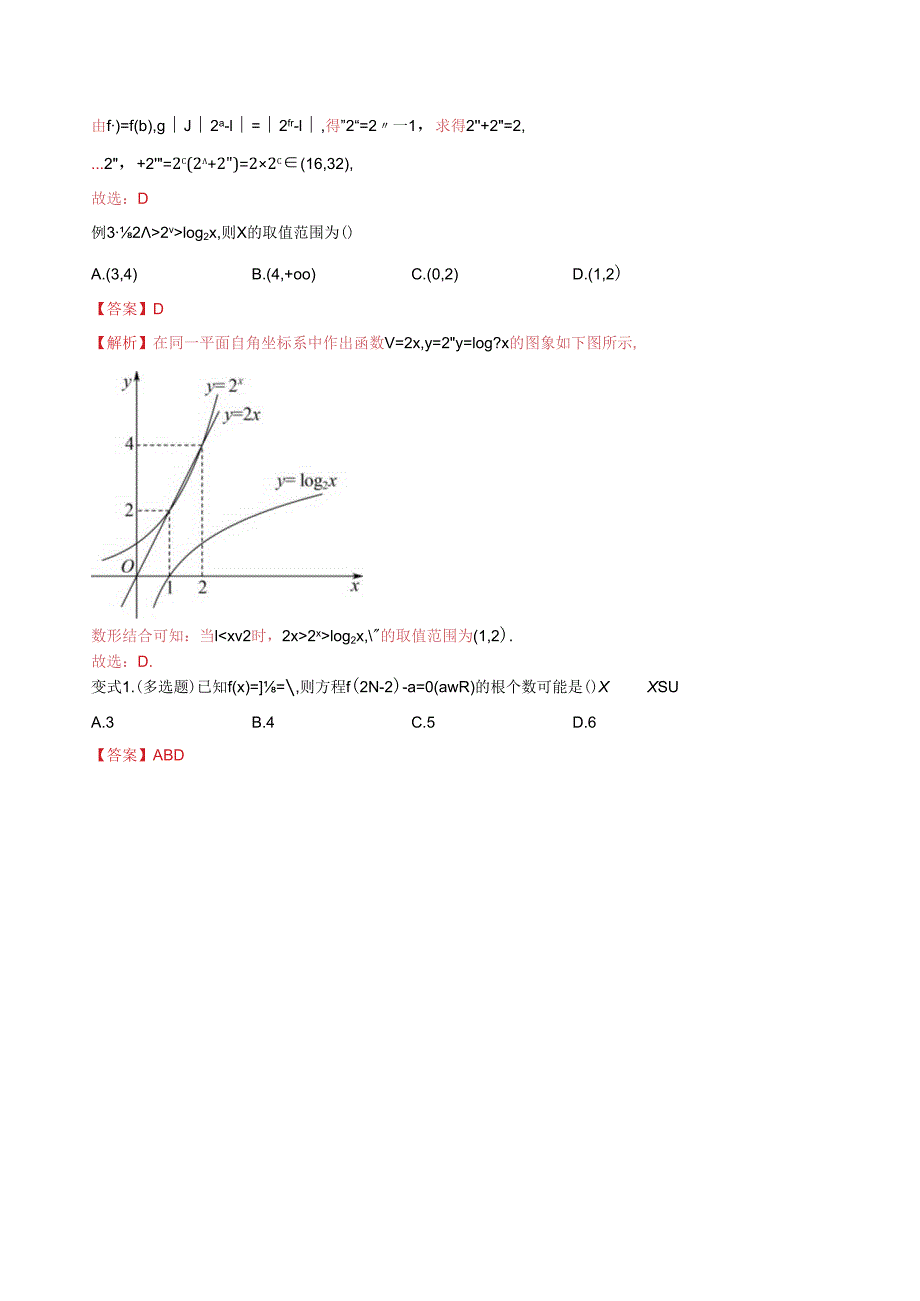
3、图象关于)，轴对称，将函数丁=则的图象向右平移2个单位长度可得函数)，=2k7的图象，所以函数y=2T的图象关于直线=2对称，故。=2.故选：B例2.已知函数/U)=2若实数,c满足b2值范围为()A.(4,8)B.(4,16)C.(8,32)D.(16,32)【答案】D【解析】作出函数/(x)的图象，如图,当v时，/(x)=2x-l=l-2x(0,l),由图可知，/（八）=()=(c)(0,l),即4-c(0,l)得3c2vlog2x,则X的取值范围为()A.(3,4)B.(4,+oo)C.(0,2)D.(1,2)【答案】D【解析】在同一平面自角坐标系中作出函数V=2x,y=2y=log?x

4、的图象如下图所示,数形结合可知：当l2xlog2x,的取值范围为(1,2).故选：D.变式1.(多选题)已知f(x)=,则方程f(2N-2)-a=0(awR)的根个数可能是()XXSUA.3B.4C.5D.6【答案】ABD【解析】令州-2=d-1),在同一坐标系中作出函数y=Q)(fT)和直线y=。的图象，分析/-a=0的根：当时，方程W-=0有一个根4,且42,方程泄-2=小对应2个X,故方程2IM-2)-=0(wZ?)有2个根；当=10寸，方程/一。=0有两个根6=T,f?=2,方程州-2=大对应1个孙方程川-2=，2对应2个4,故方程/(2M-2)-=0(eR)有3个根.当OVaVl时，

5、方程一。二0有三个根T1.0,Gl,t3D.OGel【答案】BD【解析】观察图象得，函数f()=-b是单调递减的，因此，00仃：Oyol,而X=O时，y=-bf于是得Ovl-b2B.3atZR,使得0+8lC.2+2=2D.a+b2J2“2”=26工，所以2+z*vl,则+h。)上则一+i最小值为q【答案】【解析】当x=l时，y=+l=2,.y=优-I过定点A(l,2),又点A在直线nv+y=3上，,m+2n=3,即(?-1)+2=2,rn,nO,.n-0,12+tn-n；(出+淤-2)中5+2n9=-(当且仅当含:中，即加=(时取等号),9故答案为：.变式5.函数y=/-，+7(a0,且4W

6、1)的图象恒过定点P,尸在基函数/(x)=f的图象上，则了【答案】27【解析】因为函数y=r+7(。0,且l)的图象恒过定点户,所以由指数型函数性质得尸(2,8),因为尸在弃函数/(X)=/的图象上所以2。=8，解得。=3,所以/(x)=f,/(3)=27.故答案为：27变式6.函数y=(o.5-8户的定义域为【答案】(Yo，-3)【解析】因为y=(05-8)T10.5a-8所以0.5A-80，则2-t23,即一x3,解得xv-3,故函数y=(0S-8)T的定义域为(-8,-3).故答案为：(-8,-3).变式7.已知函数f(x)=h-a的定义域为2,+co),则=【答案】4【解析】由题意可知

7、，不等式2:。“的解集为2,+00),则22-=0,解得a=4,当=4时，由2-40,可得24=22,解得x2,合乎题意.故答案为：4.变式8.已知函数,/(%)=OV+力(。0,a).(1)若大幻的图象如图所示，求出力的取值范围；(2)若兀r)的图象如图所示，1U)=m有且仅有一个实数解，求出?的范围.【解析】(D由危)为减函数可知4的取值范围为(0,1),又型)=1+XO,所以b的取值范围为(一co,-1)；(2)/的图象过点(2，),(，-2),所以+b=0a+b=-2解得=3,b=-3,所以f(X)=(G)-3,在同一个坐标系中，画出函数y=l()l和y=m的图象，观察图象可知，当机=

8、0或m3时，两图象行个交点，若l()I=帆有且仅有一个实数解，机的范围是：m=0或n3.题型二,指数(型)函数的单调性应用(1)：复合函数的值域问题例4.函数丁=42川+3的值域为一.【答案】(3,+)【解析】令2p0),.函数=4+2向+3(工/?)化为/(r)=f2+2r+3=(r+l)2+2(r0),(r)3,即函数y=412r+,3的值域为(3,+).故答案为：(W-)例5.函数y=g)*+2的值域为()A.,+)B.(,-C.(,2D.(0,2【答案】A【解析】函数y=g)+2，定义域为R,-x2+2x=-(x-1)2+11,又函数)“在R上单调递减，则严山W，所以函数)，=()-2

9、+2x的值域为g,+).故选：A例6.已知/(6=22029-2*+1(其中eR且。为常数)有两个零点，则实数的取值范围是【答案】（4,+）【解析】设f二2*（0,”），|（力=221+2川一。2+1有两个即方程产+（2-）+l=0有两个正解，=（2-a）2-40所以+q=20,解得a4,r1r2=lO即（4,+）,故答案为：（4,F8）.变式9.函数/*）=9-t+Ql+（在T*o）上的值域为.【答案】(44【解.析】人+0+：=（川+3出+：.xw,+oo）则令r=（g）（0,3y=r+3f+（在（0,3递增（375.,.ye7,v144故答案为：fpT-144变式10.方程2+3X=A的

10、解在。，2）内，则Z的取值范围是.【答案】（5,10）【解析】令y=2+3x,x（l,2）,显然该函数为增函数，2,+31=5,22+32=1O,值域为（5,10）,故50）的值域是【答案】（0,2）【解析】令，=2（0,l）,则y=+z,因为函数y=+f在(0,1)上单调递增，所以y=+f(o,2),故力的值域为(0,2).故答案为：(0,2).变式12.已知函数/(x)=ax+b(0,I),其中,b均为实数.1若函数/(x)的图象经过点A(0,2),B(1,3),求函数y=7(m的值域;(2)如果函数/(x)的定义域和值域都是1.1,0,求a+力的值.l+b=2a+b=3【解析】(1)函数

11、/(x)=ax+h(40,a)f其中,力均为实数,函数/(4)的图象经过点A(0,2),B(1,3),a=211bi，函数/（X）=2x+,函数1.11、1又K亍=2o,故函数y=j亍的值域为(0,1).(2)如果函数f(X)的定义域和值域都是1.1,0,若1,函数/(x)=Ol+6为增函数，.彳。,求得、无解.1+=0-b=0a=若OVaV1,函数/(x)=x+b为减函数，/.a,求得，2,1+/?=-1b=-2皿3a+b=.2变式13.已知函数/(=2小4叫(1)当。=1时,求/(X)的值域；(2)若/(力有最大值16,求。的值.【解析】(1)当。=1时，x)=2Mx+2因为y=2，在R上单调递增，y=2+4x+2=(x+2)2-2-2,可得2/+22-2=l,所以/(力2=；,故f(x)的值域为j+8).(2)令，=公2+41+2,因为函数y=2，在其定义域内单调递增，所以要使函数/(力有最大值16,贝h=0+4+2的最大值为4,0且0Hl)的图象经过点(-2,16).(1)求，并比较f(m2+3与/(?-1)的大小；44(2)