 17.代几综合:202405各区二模试题分类整理(教师版).docx
17.代几综合:202405各区二模试题分类整理(教师版).docx
《17.代几综合:202405各区二模试题分类整理(教师版).docx》由会员分享,可在线阅读,更多相关《17.代几综合:202405各区二模试题分类整理(教师版).docx(18页珍藏版)》请在第壹文秘上搜索。
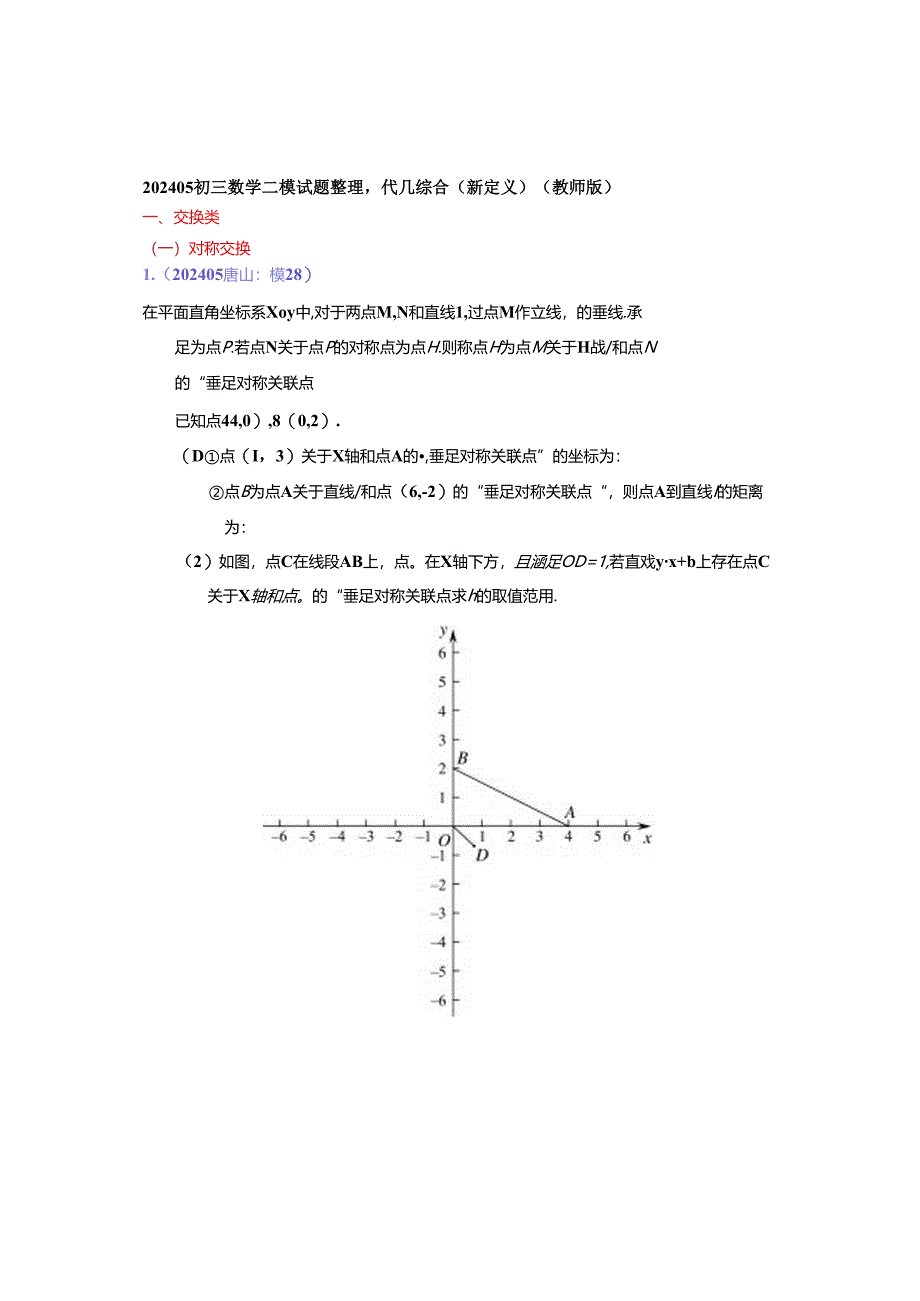
1、202405初三数学二模试题整理,代几综合(新定义)(教师版)一、交换类(一)对称交换1.(202405唐山:模28)在平面直角坐标系Xoy中,对于两点M,N和直线1,过点M作立线,的垂线.承足为点P.若点N关于点P的对称点为点H.则称点H为点M关于H战/和点N的“垂足对称关联点已知点44,0),8(0,2).(D点(I,3)关于X轴和点A的,垂足对称关联点”的坐标为:点B为点A关于直线/和点(6,-2)的“垂足对称关联点“,则点A到直线I的矩离为:(2)如图,点C在线段AB上,点。在X轴下方,且涵足OD=1,若直戏yx+b上存在点C关于X轴和点。的“垂足对称关联点求h的取值范用.(1)(-2
2、,0):2分1:4分(2)解;点。在X轴下方,旦满足8=1,;点D的轨迹是以。为暖心,1为半径在r轴下方的半圆(不包含与X轴的交点.;点。在城段AB上.过。点向X轴作垂线,垂足在X轴上,垂足的横型标的取值范围是:0x4.;.点C关于X蝌和点D的垂足对称关联点的轨迹如图所示.VH找)=x+上存在点C关于X轴和点D的垂足对称为账点,当直线y=X+Z与O相切时,半径r=1,则直线=X+/,与y轴交干(0,2).可得:=25分当直线y=x+过(9,0)时,可得:b=-96分.-9W07分2.(202405顺义:模28)在平面Hffl坐标系X)中,Xj于点,和图形”,给出如卜定义:若图形W上存在一点Q不
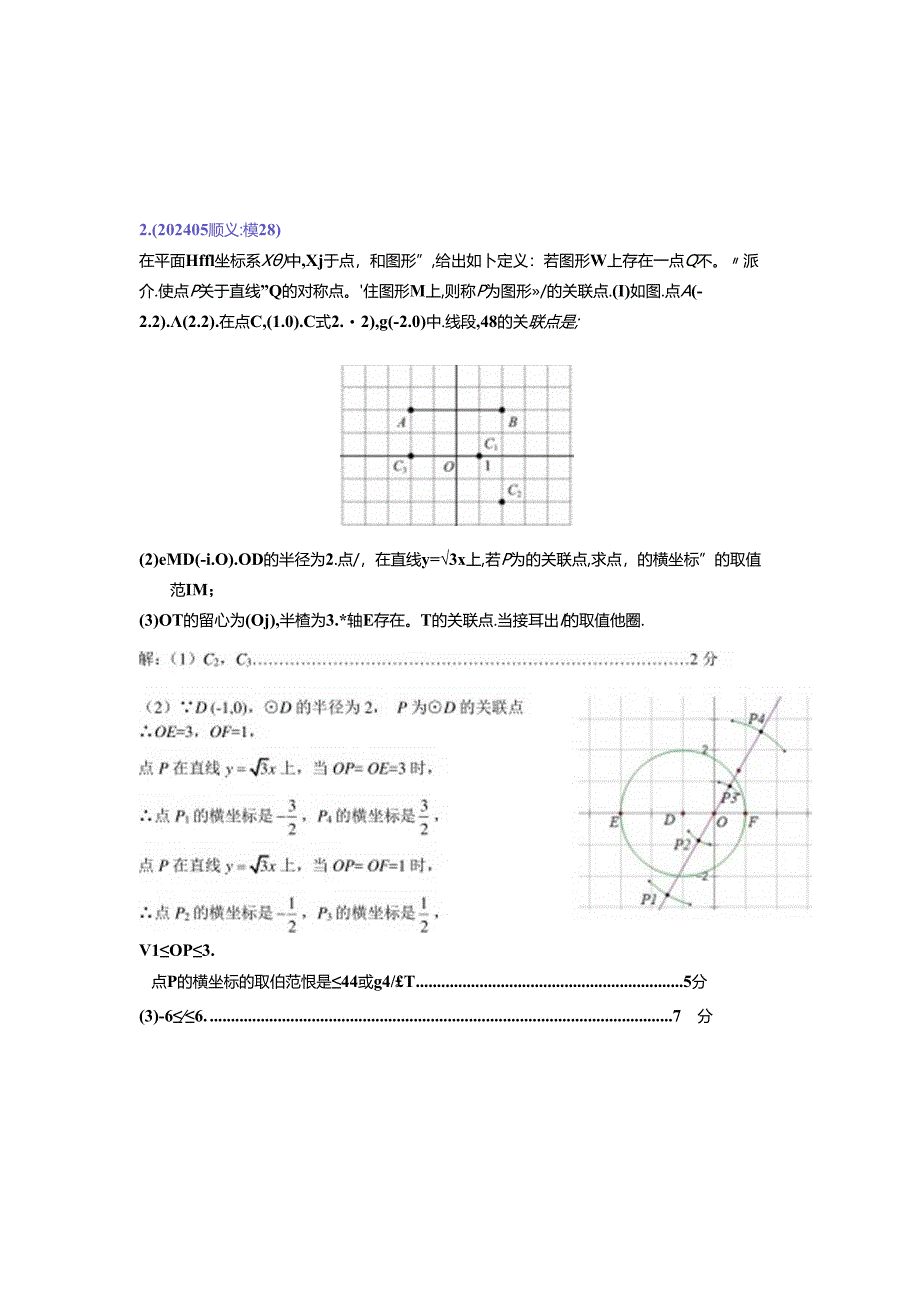
3、。派介.使点P关于直线”Q的对称点。住图形M上,则称P为图形/的关联点.(I)如图.点A(-2.2).(2.2).在点C,(1.0).C式2.2),g(-2.0)中.线段,48的关联点是;(2)eMD(-i.O).OD的半径为2.点/,在直线y=3x上,若P为的关联点,求点,的横坐标”的取值范IM;(3)OT的留心为(Oj),半楂为3.*轴E存在。T的关联点.当接耳出I的取值他圈.V1OP3.点P的横坐标的取伯范恨是44或g4/T5分(3)-66.7分二)旋转交换3.(202405西城二模28)如图I.对于。外的线段P0(线段20上的各点均在。外)和直线”?上的点N.给出如下定义:若找段PQ烧
4、点R板传某一角度得到的戏段00恰好是OO的弦.则称点R为段段PQ关于00的“割的点二在平面直角坐标系My中,。的华径为I.(DtaW2.已知点S(l,4).(-1,2).U(l,2).IK(OJ).在线段孙TU.U即中.存在关于。的“割圆点”的战段是.该“割醐点”的坐标是:(2)fly-x+经过点Jr(0.3).与X轴的交点为点匕点P.点Q都在戊段VWI:.HP=2.心线段PQ关于O的“MISizr为点R.jdl,.R的横坐标巧,的取做范典:(3)线/经过点(1,6).不电合的四个点X.B.C.DKaatHII.R点既是战段/18关于。O的“荆网点二又是线段CD关于OO的“割脚点戏段18,Co
5、的中点分别为点A,A.记线段MV的长为d.写出d的取值他用.解:UW,(2.1)s2分(2)xl-2dixjr-l:4分(3) 0d2-j或2jdv4.7分5. (202405大兴二模28)在平面百加坐标系XaY中,对于点丁,M(a.%),N5,3,给出如下定义:若点N以点了为中心逆时针旋转90后,能与点A/咆合.则称点7为线段MN的“完美等出点”.(I)如图1,当a=0,b=2,=2时,战段MN的“完美等出点”坐标是;(2)如图2,当=0.=2时,若直线y=X+2上的一点7,满足了是线段MN的“完关等直点求点T的坐标及6的值::.Z7KW-Z7lf-90o.VZ1=Z2,*Z3=Z4.V7i

- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 17. 综合 202405 各区 试题 分类 整理 教师版
 第壹文秘所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
第壹文秘所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。


 重点工作绩效评估自评表.docx
重点工作绩效评估自评表.docx
