模型10 加权逆等线最值模型（原卷版）.docx

《模型10 加权逆等线最值模型（原卷版）.docx》由会员分享，可在线阅读，更多相关《模型10 加权逆等线最值模型（原卷版）.docx（12页珍藏版）》请在第壹文秘上搜索。

1、加权逆等线最值模型模型介绍【模型感结】回在求形为“QB+kPAn(k#l)的式子聂位问题时，关键是要通过相似三角彬构造出与相等的税段(即421=Q0,将Q6+Mjl”型问题转化为t,QB+QC,型将军饮马问题,当k=l时，加权逆等线就变成了逆等或拼接最优模型，此种情况属于权为1的特殊情况，只需通过全等三角形构造出相等或段即可，然后将问题变为畲见的将军饮马问题求解即可.回需要注意：这里的QB、01两界线及的廷犬首方向必须要有交叉，方能通过相似或全等三角形得到kP的等线段.【解题方法】回利用比例线段构造相似三角形转化段段，杷双动点问题转化为单动点将军饮马问题,利用“两点之间统段我短”从而解出答案.

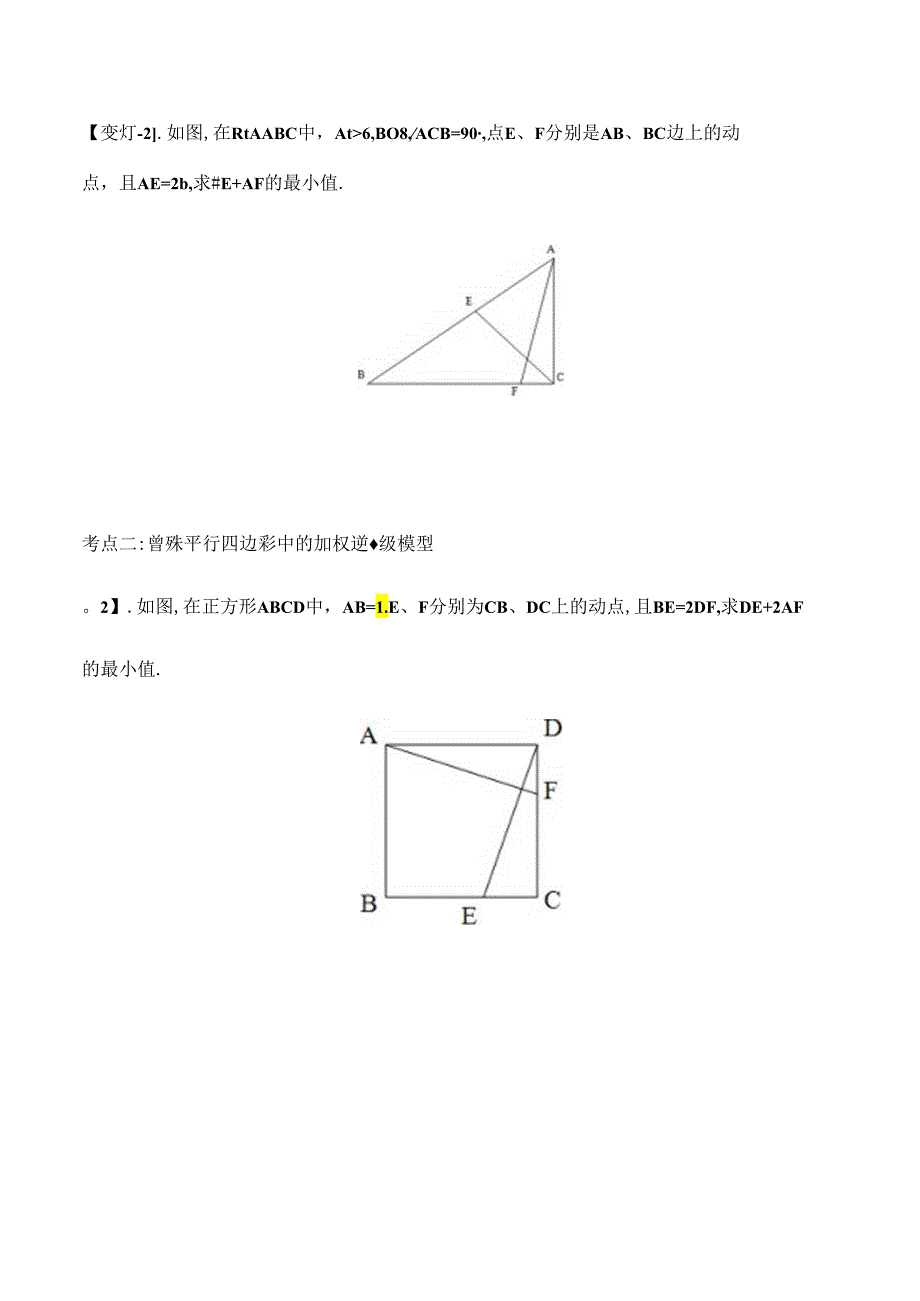
2、例题精讲考点一:直角三角彩中的加权运畿模型【记1.如图，己知BC1.AB,BC=AB=3,E为BC边上一动点，连接AE,D点在AB延长线上，且CE=2BD,则AE+2CD的最小值为多少.A变式调练【变关7】.如图，等腰直角aABC中，斜边BC=2,点D、E分别为线段AB和BC上的动点,BE=正AD,求AE+J&T）的最小值.D【变灯-2.如图,在RtAABC中，At6,BO8,ACB=90,点E、F分别是AB、BC边上的动点，且AE=2b,求#E+AF的最小值.考点二:曾殊平行四边彩中的加权逆级模型。2】.如图,在正方形ABCD中，AB=1.E、F分别为CB、DC上的动点,且BE=2DF,求D

3、E+2AF的最小值.，交式调峰It2-U如图,在矩形ABCD,D=4,B=43,点EJ-分别是BD,BC上的一动点，且BF=2DE,则AF+2AE的最小值为多少？【变式2-2.如图，在菱形4%中，NBAD=I20：。=4,M川分别是边的，力。的动点，满足内仁必；连接CMCV,6,是边GV上的动点，厂是CW上靠近C的四等分点，连接/区、BE、NF,当aw面积最小时，/砂力的最小值为.C1 .如图，等腰Zsabcnbac=no.ab=ac=，D、E分别是AB、BC边上的动点，I1.满足BE7d,求AE+辰D的最小值.2 .如图，.M为矩形；中加边中点，E、广分别为砥、上的动点，11.BE=2DF,

4、Aff=I,BC=2,WWR2/的最小值为3 .如图，在正方形械中，为上一点，且（E、尸分别为儆比上的动点，且BF二3DE,若力=3求*+3/庐的最小值.4 .如图，在RtZO,%4=9O,/月=30,心=,点在线段加上，点在线段府的延长线上，JlBE=AD,则出8的最小值是.5 .如图，在矩形40中，B=A.M=6,点/在边力。上，点。在边呢上，且朋=卬，连接CP,则凡%的的最小值等于6.如图，平行四边形月比仇4MZH4,ZJZW=60,E、尸为对角线加上的动点,DE=tIBF,连接月、CF,则/2。1的最小值为B7 .问题提出:（1）如图，在正方形/版Q中，6为边仍上一点（点6不与点4、方

5、至合），连接应；过点/1作Af-1.DE,交a于点/；则DE与的数量关系是：DEAfi问题探究：2）如图，在矩形用%刀中，AB=4.36,点E、尸分别在边,很上，点0为线段EFk动点，过点作仪的垂线分别交边/久犯于点6、点.若线段恰好平分矩形/收？的面积，且游=1,求G”的长；问题解决：如图，在正方形械。中，/为初上一点，嚼V夕分别为必上的动点且BE=2DF,若Aff=A,求世,2/的最小值.图图图8 .如图，在4i欧中，ZAC=60,BC=6,北-8,D、分别为边/亿；/团上两个动点.（1）如图I，若为47中点，且龙平分胸的周长:i）求E-尿的值：ii）求证：AEg300,并直接写出原的值：

6、=a,将线段力绕点/1按逆时针方向旋转a得到仍连接阳SE,BR(I)求证：/蜂的1：(2)如图2,若NaM=90,ZACD=AOo,旦点从E、尸在条直线上，求“*,的值：(3)当OB=OC、ACD=IM,密毋长的最小值是.(I)如图I,已知NW90.若DR=B,求证：四边形Z心丫为平行四边形：(2)如图2,已知/4仁60.若班为/1落的角平分线，7为线段SV上一点，W的延长线交线段展于点M满足：IUnsw=J且小上布请认真思考中图形，探究黑的/AD值.)的最小值为.11.如图，在菱形/收？中，N阴P=I20,/15=6,连接打.1）求如的长；,点尸在边力上，且BnMDR当行US时，求四边形/!戚的面积：当四边形4班F的面积取得最小值时，由的值是否也最小？如果是，求CEf3CF的最小值：如果不是，请说明理由.