模型03 全等三角形中的常见五种基本模型（解析版）.docx

《模型03 全等三角形中的常见五种基本模型（解析版）.docx》由会员分享，可在线阅读，更多相关《模型03 全等三角形中的常见五种基本模型（解析版）.docx（36页珍藏版）》请在第壹文秘上搜索。

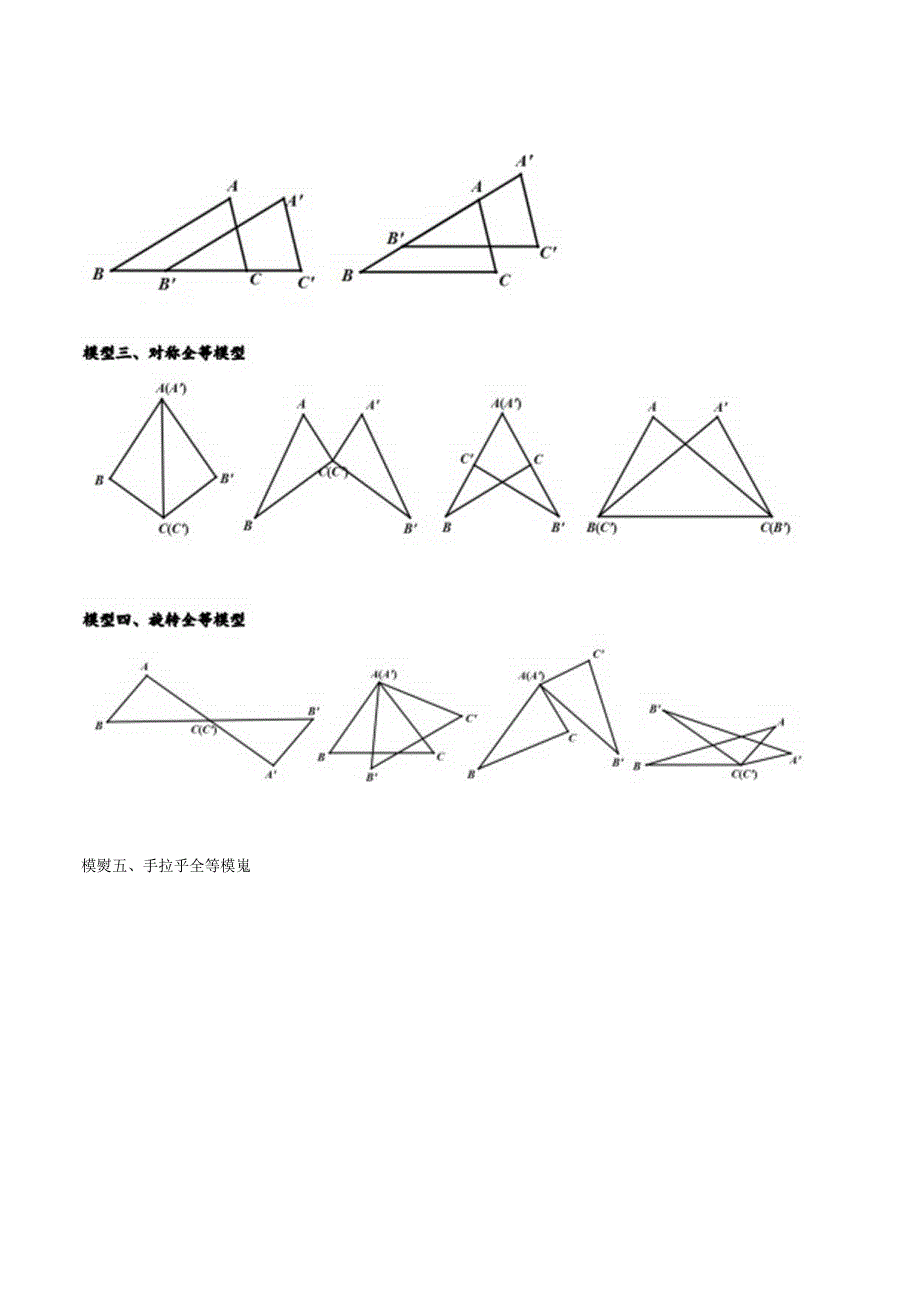
1、全等三角形的常见五种模型模型介绍全年三处形的撰型种臭多，其中有关中点的模型与季立梯型在料面的专题已拄很洋统的讲解，这里就不在支复.模型一、横长：在较长的战段上极取另外两条.核处的畿段。如图所示，在BF上极赧BM=OF.%tiBMCSDFC(SAS)1；MC=FC=FG,ZBCM=ZDCF,可得AMCF为号膜近角三角彩.义可证NCFE=45.ZCFG=90o,ZCFG=ZMCF.FGCM.可得旧边形CGFM为平行E边形.JCG=MF.于是BF=BMMF=DF*CG.科短：选取两条枝短域段中的一条进行延长，使用较短的两含蝶我共伐并寻求解麴突破。如图所示.廷长GC至N.CN=DF.为证4CDFgZB

2、CN(SAS).可祥CF=FG=BN.ZDFC=ZBNC=I351.又知NFGC=45,可证BNFG,于是四边形BFGN为平行四边形，BF=NG,所以BF=NG=NC+CG=DF+CG.模熨五、手拉乎全等模嵬例题精讲【例1.如图.AD工BCAB+BD=DC.ZB=54.则NC=27.BZZDCbd2C解：在DC上被取DE=6连接A,VD1BC.DE=BD,及HE的垂直平分处，：.AB=AE.Z=Zf=54.AB+BD=DC,DE+EC=DC,AB=EC9JAf=EC,ZC=ZE4G.C+NEAC=NA8=540ZC=ZEAC=-IZE=27.故答案为：2T.2A变式训练【变武I-IJ如图点是Z

3、XABC三个内角的角平分线的交点连接AHB=BC,则NCm的度数为B.AO=CO.8。平分/4BC,求证：NA+NC=1M).证明:在缱段BC上取BE=4,连接DM如图所示.丁8。平分/4BC.,.Zahd-Zebd.AB=EB6.ahi)f4tw.Zabd=ZEBD.BD=BD.ABDEBD(S5,；.AD=ED,ZA=ZBED.JAD=CD.：.ED=CD.：.ZDEC=ZC.VZtfEZX-ZDEC=IHO.二NA+/C=I80”.【变武1-3】.ll.AA8C为等腰直角二角形,AB=ACNSAC=90.点/)在线段48J1.,连接CdZADC=60,.AD=2.过C作Cfi1.C).H

4、C1.=CD.连接/)交,BC干F.=CDCE=-44S.22(2)证明：在EF上取一点M.使得EM-ZJR：EC=CD.ZE=ZCDF=AS,:ZCM9ADCF,：.CM=CF,VADC=W,ZFDtf=180-60-45=75.ZUbB=ZCFM-180-75t-45=60.二ACFM是等边三角形，：.CF=MF.二EF=EW+AfF=DF+CF.模型二、平&金等模型【例2】.如图,在四边形ABa）中,E是AB的中点,AD/EC.ZAED=ZB.1求证：AAED坦AEBC.2当A8=6时，-Cz）的长.(I)证明：,.,ADEC.，Z=ZBEC.；是A8中点，.,.AE=EB.：ZED=N

5、B.EDEBC.2)解：.,Af-DEBC.：.AD=EC.：AD/EC.四边形AC7)是乎行四边形,：.CD=AE.；八8=6.CO=4八8=3.2A变式训练【变式2-11如图l.B,C.D在同一B1.我上,A8=CZ）,DE/AF,DE=AF.求证：AFCDEB.如果将8沿着A。边的方.向平行移动，如图2,3时，其余条件不变，结论是否成立？如果成立，请予以证明：如果不成立，诂说明理由.耨：AB=CD.AH+BC=ClHC.JCBD.：DE/AF,AF=DEH4FC和中.(ZA=ZD-AC=DB：.AAFC迫ADEB(SAS).在2).(3)中结论依然成立.如在3)中，AB=CD.AB-BC

6、=CD-RC,WAC=BD.7AFl)E.A=NO.AF=DE在八b和/)中，Za=Zd.AC=DB4CF52DESAS).(A2-2.如图,AD,相交于点O.AR/DF.AR=DF.点E与点C在M上，且M=CE I)求证：AABC沿ADFE：2)求证t点。为BF的中点.二NB=ZF.,:BE=Cf-.BCEF,在八8C和AOFE中,AB=DFZb=Zf.BC=EF.ABCDFECSASh：.AC-DE.ZACB=NDEF.iACO和aDEO中.Zacb=ZDEFZaoc=Zdoe.AC=DE二八COg。卬（AAS）,：.EO=CO.点。为M的中点.【变式2-3.如图，XA08和ACOO均为等

7、腰直角三角形，NA。=NCO。=90”，。在A8上. 1）求证：dAOCSB0D;TiAD=1.ADC=60,求CD的长.证明：FAO8和ACOD均为等腰直角三角形,.ZAOB=ZCOD=90,OA=OB.OC=OD.：./BOD+/AOD=N,/AOC+/AO/）=90.：.ZBOD=ZAOC.4tX?和ABC/）中.rCO=DOZbod=Zadc.OA=OB.OC2flOD（SSh解：.,OOOD.：.ZCAO=DRO=45t.又8A=45.CAQ=90,VAD=I.ZADC-60.D=2AD=2.【例3】.如图，AO8C.ZD=90o.CPB=W.NDAB的角平分线与NCgA的角平分级相

8、交于点P.且。,P.C在同一条宜线上.1）求N0的度数：解：,.,DBC.ZC=180-ZD=180,-90=90*，:NaI8=川：.ZPBC=90-/8=60.,：PB平分/ABC.：.NABC=2ZPBC=120.7ADBC.ZDB+ZC=I8O,.：.ZDAB=SOa-120=60,.YQ平分/)AB.ZPAD-ZDA30,:2,E分别是Af1.AC的中点.AMA.CD=M.AAC1.BE干M求证：八M=AM解：.Y8=AC,D.E分别是八8、AC的中点,：.ADBD=AE=EC,NB=NC,在/)BC和/?/C中BD=ECZB=ZCBC=CBDCEBC.NBDC1.ZBDE.：N8D

9、C=NAfW,ZfifC=NAEN,：.ZADM=NAEN,在ZXawo和Zsane中Zamd=Zane=OOoVZadm=ZaenAD=AE.MDNEAM=AN.【变式3-2.如图.已知点F分别是正方形ABC7中边AB、8C上的点，HA8=12.AE=6,将正方形分别沿DE./”向内折会.此时DA与DC理合为DC.求CF的长度.解：设(T=X,则FG=x.FB=I2-X,：AH=n.A=6.：.BE=6.EG=6.工EF=Xx在RlBfF,BEB户=E产.62+(12-2=(.r+6)2,x=4.即CF的长为4.【变式3-3.如图，ZOB=9Q,OM平分NAo8,将直向三用板的顶点P花射线O

10、M上移动，两宜角边分别与。A、。8相交于点C、。，何PC与/，。相簪吗？试说明理由.解：/C与PO相等.理由如下：过点P作PE1.OA于点E.PF1.OB千点F.=CM平分/AC8.点P在M上.PE1.()A.PF1.OH.IPE=PF(用平分线上的点到角两边的距离相等)XVZAO=90j.NPEO=NPFO=%,：.四边形OEfT为矩形,；./EPF=9()：./EPC+NCPF=W,又.CP)-90.：.ZCPF+ZFPD=W*.NEPC=NFPD=X)-ZCPF.在尸CT与以)尸中，ZPEC=ZPFd；PE=PF，ZEPC=ZfpdPCZiPDASA).：.PC=PD.【例4.如图，已知

11、：A)=48.AE=AC.AD1.AH.AE1.AC.猜想线段。与之间的数让关系与位置关系,并证明你的猜想.解：Jftffi=CD=BE,CD1.BE.理由如下：AD1.AB,AElAC.M=ZE4C=90.,.,DAR+ZRAC=E4C+ZRAC.RPZCAD=ZE4.住ZiACO和ZkAtW中.AD=ABZcad=Zeab.AC=AECD!E(AS).1.CD=BE,NADC=NASe,；NAGD=WFGB.：.NBFf)=NaAD=9()：即CO_1.8A变式训练【变式4/1己知AA8C和AAOE均为等膻三角形，且8AC=NZME,AB=AC.AD=AE.(1如图1,点E在8C上，求证；BC=BD+BE;(2如图2,点E在CB的延长蜿上，求证：RC=HD-BE.I)证明：VZfiAC=/DAE,：.NBAC-ZBAE=ZDAE-NBAE.ZDAB=ZEC.