23年二模定理证明汇编.docx

《23年二模定理证明汇编.docx》由会员分享，可在线阅读，更多相关《23年二模定理证明汇编.docx（10页珍藏版）》请在第壹文秘上搜索。

1、O1.23.模海淀/怀念密云】19.如图，iZJC,B=C.使用直尺和圆规,作A1.）BC受BC干点D（保留作图痕迹）：2）以D为圆心，OC的长为半径作版，交AC于点连接DE.NBEC=；写组图中二个与/CW：相等的角.02123二枚西城/通州/延庆】419.已知:如图1.线段.b.求作；矩形八BCZX使得A8=,BC=b.作法：如图2.图I1 .在互线/上械取A8=2 .过点8作出规，”_!_/，在直雄，n上故取=A.3 .分别以点A和点C为圆心.从“的长为半径而孤.两孤的交点为/）.（点。与点C1在宜线/的同侧j4 .连接/UCD.Aa则四边形八8C。为所求的矩形.图2根据上面设计的尺规作

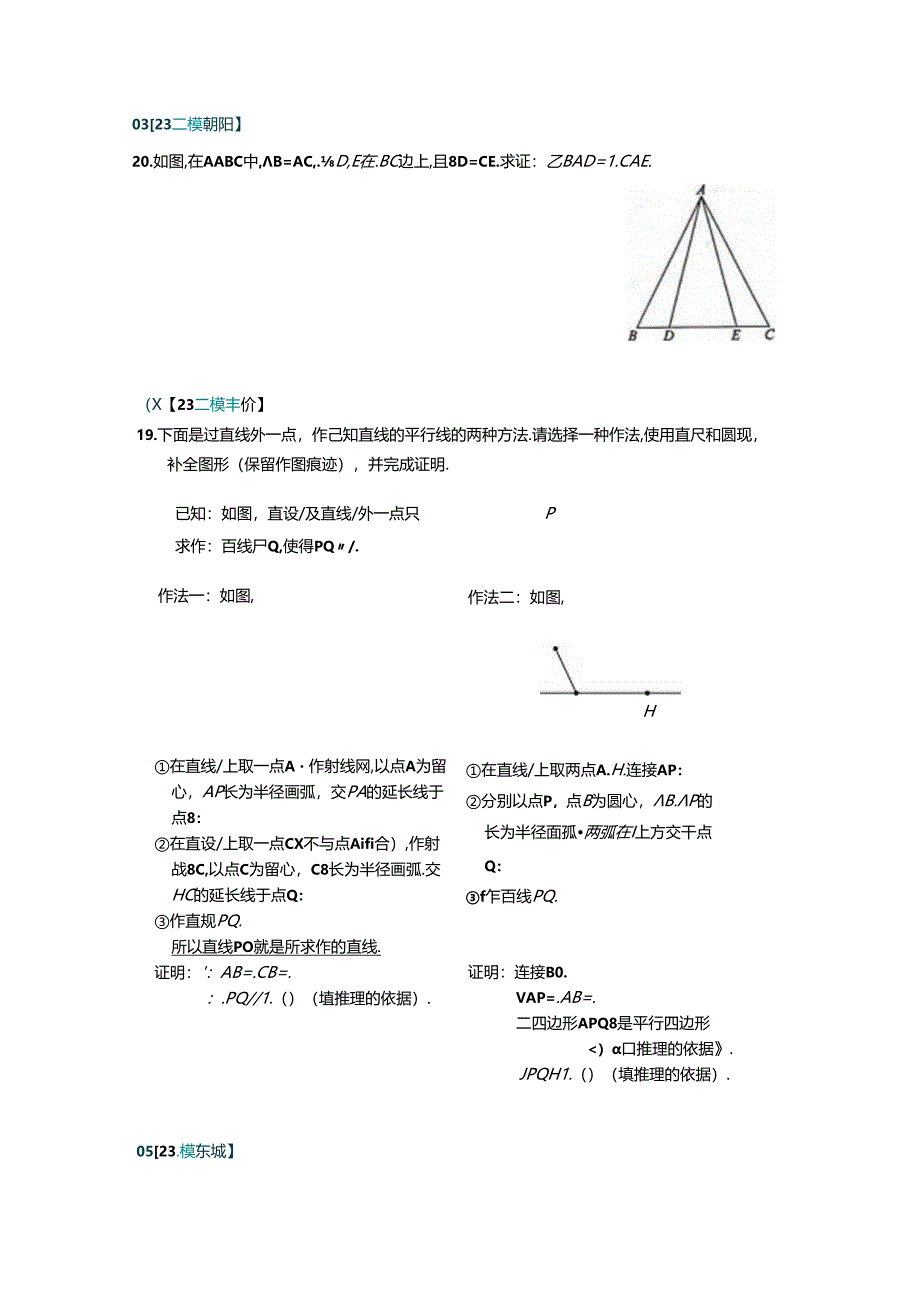
2、图过程，（I）使用直尺和10观，在图2中补全图形（保胡作图痕迹）：（2）完成下面的证明：证明：VD-BCh.BDC=a.四边形A8C/）是平行四边形（）.（域推理的依据.直线n/.ZABC=.二四边形A8C/）是矩形（）.（埴推理的依据）.0323二模朝阳】20.如图,在AABC中,B=AC,.D,E在.BC边上,且8D=CE.求证：乙BAD=1.CAE.（X【23二模丰价】19.下面是过直线外一点，作己知直线的平行线的两种方法.请选择一种作法,使用直尺和圆现，补全图形（保留作图痕迹），并完成证明.已知：如图，直设/及直线/外一点只P求作：百线尸Q,使得PQ/.作法二：如图,作法一：如图,H在

3、直线/上取一点A作射线网,以点A为留心，AP长为半径画弧，交PA的延长线于点8：在直设/上取一点CX不与点Aifi合）,作射战8C,以点C为留心，C8长为半径画弧.交HC的延长线于点Q：作直规PQ.所以直线PO就是所求作的直线.证明：AB=.CB=.：.PQ/1.（）（埴推理的依据）.在直线/上取两点A.H.连接AP：分别以点P，点B为圆心，B.P的长为半径面孤两弧在I上方交干点Q：f乍百线PQ.所以直线PQ就是所求作的直线.证明：连接B0.VAP=.AB=.二四边形APQ8是平行四边形三60o. AB=AB.CBADB()(域推理的依据).ACB30.0823二模房山】20.下面是晓彤在证明

4、“平行四边形的对角相等”这个性质定理时使用的.种添加辅助线的方法,请你选择其中一种,完成证明.09123二模吕平】19.用尺埋”三等分任0ff是数学史I:-个著名她题.它t1.经被数学家他罗瓦加近世代数和论证明是不可能的.但对于特定度数的已知角.ta90offi,45。角等.是叫以用尺规进行：等分的.下面是小明的探究过程：已知：如图I.乙）3=90。.求作：9mOE.W：等分乙4。也AAJOB0cB图I图2作法：如图2.在射线，用上取任一点Ci分别以.c为Iw1.心.位:长为半径画版,两弧在，加上方交r点心（f,onrh交于点心连接CR直线SF交OC广点：以为随心.。“长为半校作圈.交线段CK

5、F点G（点。不与点，用合）；作射线-OE.所以射线OG.OE即为所求射线.（1）利用宜尺和圆规.依作法补全图形（保留作图痕迹）；（2）完成下面的证明.证明:.OE=0(：=CE,.ACOE为等边三角Ja.乙CMf=6().()H=(B-ZCOE=30.；为的M隹.Z.CCO=.乂；OE=OC,0GEC,）（炉推理的依据）.。C平分乙C(-.1.COG=乙KOG=；4COE=30.1.AOE=COG=EO(即射线OE,OG三等分乙AOB.IO23.模门头沟】19.下面是小亮同学设计的“作三角形一边k的高线”的尺规作图过程.己知：如图，/切C.求作：战段8尸，使BPUC于P.作法：分别以乐C为Bi

6、心，大于的同样长为半径作瓠.两犯分别交于点。.作比线0E.交8C于点Q以。为18心，。8长为半径作圆，交4C于点尸；连接RP.线段8P为所求的线段.根据小亮同学设计的尺规作图过程，1）使用宜尺和圜规,依作法补全图形（保宙作图痕迹）：2）完成下面的证明.证明：连接08.DC.EB.EC.：DB-DCEB-EC.DE垂直平分战段aXm推理依据）.二点。是线段BC的中点.8C是。的良径.BPC=*）（填推理依据）.：.BP1.AC.I1.123二模石景山】19.已知：如图I,直线及XB外一点尸.P求作：俄尸0,使内尸0/B.作法：如图2.布衣线48上任取点C.连接K；图1以点C为粉）心，PC氏为半径

7、作蜘，交anABJjSD,分别以点p,力为阴心.pc作孤，西孤住直线/8外交J：点01作（线P0.衣线。就是所求作的汽线.1）使用自尺和阴规，依作法补全图形保留作图双遗（2）完成卜曲的证明.ifJh连接。QVCD=DQ=PQ=，.四边膨Pa）O是膨（乂埴推理的依据）.；.PQAB.1223.模箧山】19.下面是小东设计的“作三角形一边上的Ir的尺册作用过程.已知：AABC.求作：边BC上的第AC.作法:如国I,以点A为网心，适当长为芈泾反孤，交近理BC分别以点MN为即心，以大亏MN的长为半千点M,N:西弧，两弧相交千点P（不同于点A）：作直线AP史BC千点。.所以线段A/）就是所求作的AABC的边8C上的高.根据小东设计的尺规作图过程，（1）使用直尺和13规,补全图形（保留作图痕b:（2）完成下面的证明.证明：连接八M,AN.PM.PN.AW=.PM=）（填推推的依据），.A尸是线段MV的垂直平分纹一：.AD1.BC千点D.即线段AD为AAbC的边BC上的高.