二次函数练习题及答案.docx

《二次函数练习题及答案.docx》由会员分享，可在线阅读，更多相关《二次函数练习题及答案.docx（7页珍藏版）》请在第壹文秘上搜索。

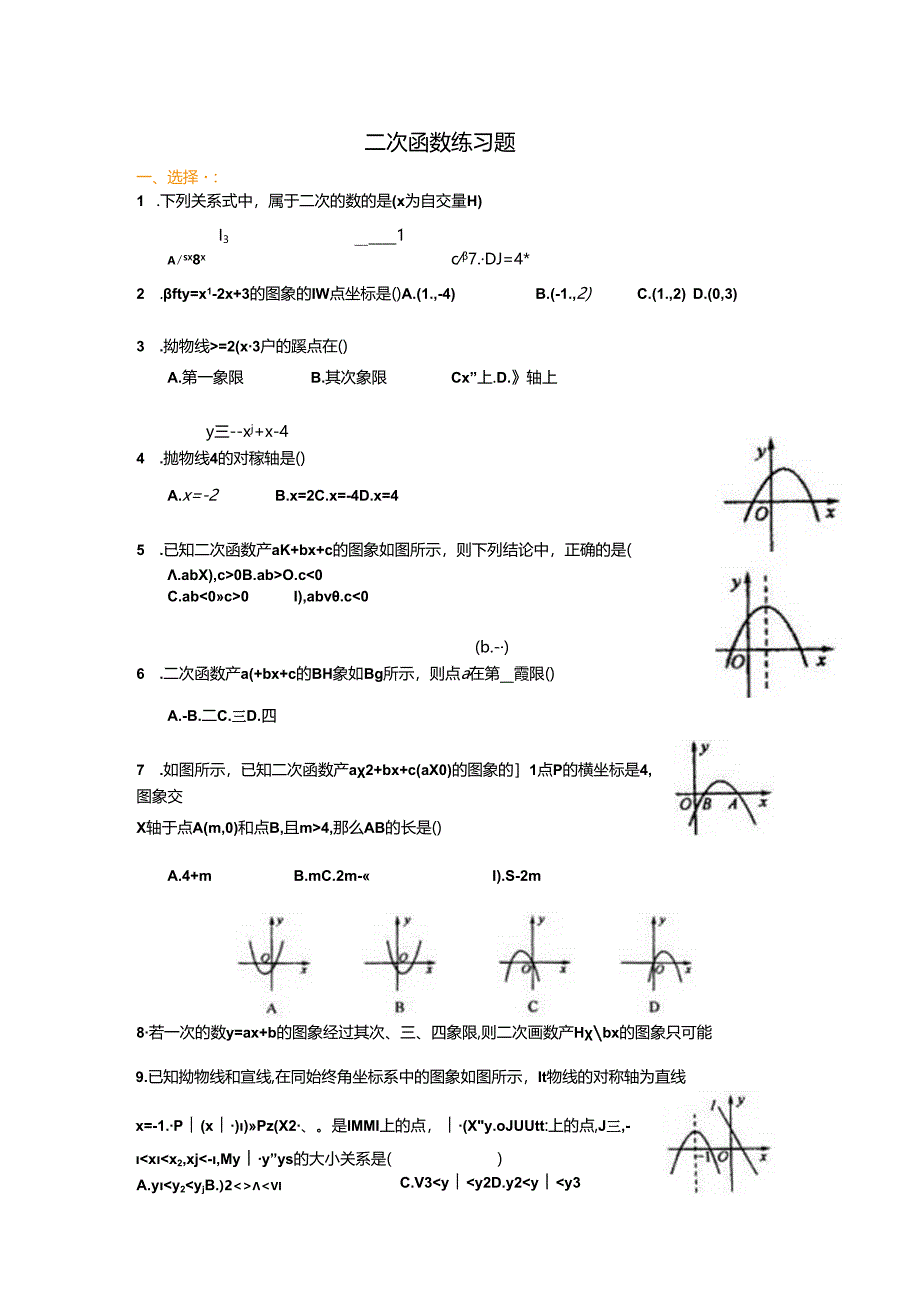
1、二次函数练习题一、选择:1 .下列关系式中，属于二次的数的是(x为自交量H)I31asx8xc7.DJ=4*2 .fty=x1-2x+3的图象的IW点坐标是()A.(1.,-4)B.(-1.,2)C.(1.,2)D.(0,3)3 .拗物线=2(x3户的蹊点在()A.第一象限B.其次象限Cx”上.D.轴上y三-xj+x-44 .抛物线4的对稼轴是()A.x=-2B.x=2C.x=-4D.x=45 .已知二次函数产aK+bx+c的图象如图所示，则下列结论中，正确的是(.abX),c0B.abO.c0C.ab0I),abv.c4,那么AB的长是()A.4+mB.mC.2m-I).S-2m8若一次的数

2、y=ax+b的图象经过其次、三、四象限,则二次画数产Hbx的图象只可能A.yy2yjB.)2viC.V3yy2D.y2yy39.已知拗物线和宣线,在同始终角坐标系中的图象如图所示，It物线的对称轴为直线x=-1.P(x)Pz(X2、。是IMMI上的点，(Xy.oJUUtt:上的点,J三,-xx2,xj2+k的形式，My=.13 .若抛物线尸J2x3与X轴分别交于A、B两点，Mab的长为.4.Ii物线y=x2+bx+,经过A(-1,O),B3,。两点,则这条飨物线的解析式为.15 .已知二次函数y=axj+bx+c的图加交X轴于A、B两点，交y*于C点，且ABC是直角三角形，请写出一个符合要求的

3、二次函数解析式.16 .在Je离地面2m商的某处把f体以初速度v11(ms展宣向上抛物出,在不计空，阻力的状况下,其上上升度s(m与抛出时间t潴意，=一不(其中K是客数,通常取IomA，).若Va=Ioms,如该物体在运动过程中商点距地面m.17 .试写出一个开口方向向上，对称轴为直线x=2,且与y轴的交点坐标为阳，3)的抛物线的#WsWj.(瓦二)和(TM)18 .已知Ii物线y=e+b2经过点4,则”的僮是.三、：m319 .若二次函数的BH象的对称轴方程是2,并且图象过Z0,4和B(4,0),(1)求比二3次函数图象上点A关于对春轴-5对称的点A的坐标I(2)求此二次函数的解析式I20

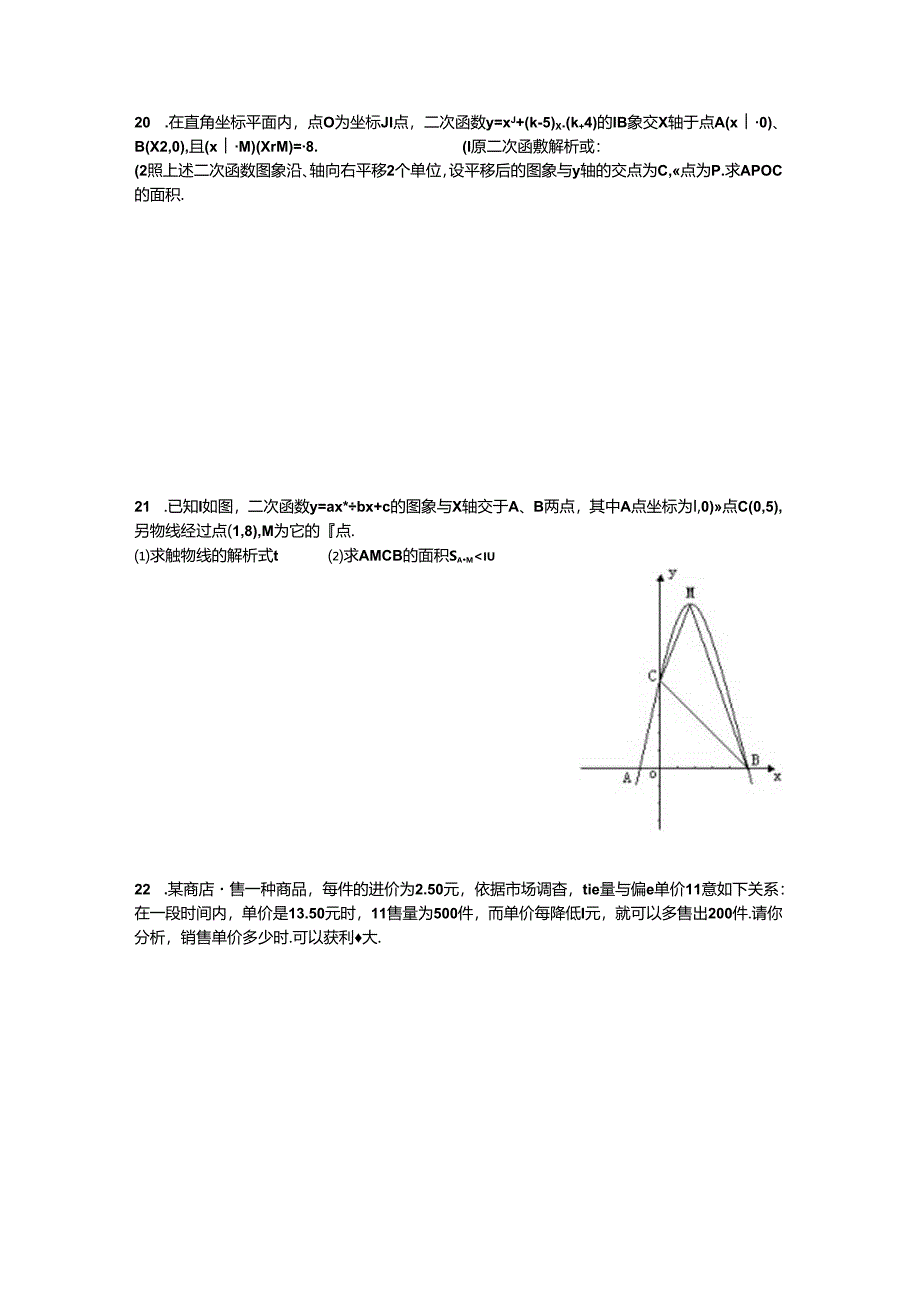
4、.在直角坐标平面内，点O为坐标JI点，二次函数y=xJ+(k-5)X.(k+4)的IB象交X轴于点A(x0)、B(X2,0),且(xM)(XrM)=8.(I原二次函敷解析或：(2照上述二次函数图象沿、轴向右平移2个单位，设平移后的图象与y轴的交点为C,点为P.求APOC的面积.21 .已知I如图，二次函数y=ax*bx+c的图象与X轴交于A、B两点，其中A点坐标为I,0)点C(0,5),另物线经过点(1,8),M为它的点.求触物线的解析式t求AMCB的面积Sa.miu22 .某商店售一种商品，每件的进价为2.50元，依据市场调杳，tie量与偏e单价11意如下关系：在一段时间内，单价是13.50

5、元时，11售量为500件，而单价每降低I元，就可以多售出200件.请你分析，销售单价多少时.可以获利大.答案与解析I一、选算1考点，二次的数概念.选A.2 .考点I求二次函数的II点坐标.Wfi法一，干用二次函数点坐标公式求.法二，将二次函数解析式由一般形式转换为点式，即yua(xh)k的形式，点坐标即为(h,k),y三x2-2x+3=(x-1.)z+2,所以1点坐标为(1.2),答案划C.3 .考点I二次函数的图象特点，点坐标.解析，可以干由JI点式形式求出J1.点坐标进行推断，函敷y=2-r答案选B.2x(-Q5 .考点I二次函数的图SI特征.解析，由图象，拙物线开口方向肉下，40,XV0

6、,0答案iC.6 .考点，数形结合，由抛物线的图效特征，确定二次函数解析式各项系数的符号特征.解析，由图象，拙物线开口方向向下，0,XVa0.器物线对称轴在y轴右2ac0,-点，由图知，该点在轴上方，(.-)a在第四象限，答案选D.7 .考点，二次画数的图象特征.解杭因为二次函数产aC+bx+c(aO)的图北的点P的横坐标是4,所以抛物线对称轴所在直线为x=4,交轴于点D,所以A、B两点关于对称轴对称.因为点Zm,0),且m4,所以AB=2AD=2=2m8,答案选C.8. 考点：皴形结合，由函数图象确定函数解析式各项系数的性质符号，由函敷解析式各项系数的性质符号出函数图象的大致秘.解析，因为一

7、次函数y=axb的图象(Kb0,-0过其次、三、四象限，2。所以二次函数y=av+M的图象开口方向向下，对禽轴在y轴左便，交坐标轴于(0,0)点.答案选C.9.考点，一次通数、二次函数概念图象及性质.解析，因为触物线的对称轴为宜战x三-,且.1-时，由图象知，yKX的地大面派小,所以立勺“又因为人J,此时点PVM”八)在二次函数图象上方,所以y2yy,.答案选D.1. .考点，二次函数图象的改变热物线=-2+4x+1.=-2(X-+3的图象向左平移2个单位得到2。+1)+3,再向上平移3个单位得到2(x+1.)+6.答案选C.二、11. 考点：二次的数性质.解析：二次函数y=2-2x+1.,所

8、以对称轴所在直线方b-2.X=I程如2.答案=1.12. 考点：利用配方法交形二次函数解析式.解析Iy=-2x+3=J2x+1.)+2=*1.)+2.答案y=f-1.)j+2.13. 考点，二次函数与一元二次方程关JR解析：二次函数产K2.3与、轮交点A、B的横坐标为一元二次方程、22x3=。的两个祗求得xt=1.xj=3,JUAB=Mx|=4省案为4.14. 考点I求二次函数解析式.-6+c三0解杭因为拗物线姓过A(1.0),B(3,。)两点，S+劝+CMOmb=】，c=3.答案为y=x123.15. 考点I此题是T开放黑，求解#B条件的二次函数解析式，答案不唯一.解析：需清意出物线与轴交于

9、两点，与y轴有交点，及AABC是亶角三角形，但没有确定事个角为宣角，答案不唯一.如：尸产.16. 考点二次函数的性质，求大值.解析I干腌代入公式，答案，7.17. 考点，此是T开放J，求IH1.废条件的二次函皴解析式，答案不唯一.解析：如ty=x24x+3.18. 考点二次函数的IK金性质，求值.提示:；a+a+b1.：aj+a+-+ba=O.(a+-)a+ba=O)答氟4442三、MB19. 考点，二次函数的假念、性质、图象，求解析式.Wr(I)A-4)20.考点：二次函数的概念、性朋、图象，求解析式.解析；由已知,*是2+(k5)x(k+4j=0的两根fx1.+x3=-(k-5)x1Xj=

10、-(k+4)又.(x+1.)(XrM)=8k+4)-(k-5)+9=0由已知平移后的函数!惭式为，且30时产.5C(0,-5).*.XXj+X+Xj)+9=0：k=5*y=x2-9为所求y=(x-2)2-9，P(2,-9)=152=5221.解：(1)依M*:a-b+c=0,a=-1.c=5解得X=抛物线的解析式为产，XX+5a+b+c=8c=5令N=O,W(x5)(x+1.)=0x=5X2三1.*B(50)由y=X+4x+”(X2)+9,气M(2,9)可得SAMCB=15.作MEJ轴于点E,则)ACB=ffWBN21EMSMaB22.思路点拨I通过四读，我的可以知道，商品的利滴和售价、第售,

11、有关系，它们之闾呈现如下关系式I总利消=单个商品的利消乂浦售金.襄获得量大利润，并不是单独提肉单个商品的利涧或仅大提商销售量就可以的，这两个，之间应达到某种平衡，才能保证利海大.因为已知中蛤出了商品降仰与商品销售抬之闾的关系，所以，我们完全可以找出总利涧与商品的价格之间的关系，利用这个等式找寻出所求的问,这里我们不妨设每件商品降饰元，商品的售价就是135X)元了.单个的商品的利润是(35.23这时商品的第倍H(500+200x)总利润可设为元.利用上面的等关式，可得到y与X的关系式了，若是二次函数，即可利用二次函敷的学问，找到量大利涧.*设销倍单饰为降价X元.则三G35-x-25)(500+200x)=(II-XX500+200x)5500+220OX500X200X-200xa+1700x+5500求助二200+7。OX+5500的顶点坐标:2-3J=4252a2(-200)44(-200)4ac-b24(-200)5500-(1700)a，“三y】/点坐标为U25,9112.5).即当每件商品降价4.25元，即售价为13.5425=9.25时，可取得大利涧9112.5元