“双勾函数”的性质及应用.docx

《“双勾函数”的性质及应用.docx》由会员分享，可在线阅读，更多相关《“双勾函数”的性质及应用.docx（7页珍藏版）》请在第壹文秘上搜索。

1、“双勾函数的性质及应用问题引入：求函数.Y=X2+5G+4的最小值.问题分析：将问题来用别禺常数法处理得，y=4+1=?+4此时如果利用均侑不等式，等式成立的条件为而JF+4=tI+4显然无实数解,所以“=不成立，因而最小但不是2，遇到这种问物应假设何处理呢这种形式的南数又具有何特征呢是否与我们所熟知的函数具有相似的性质眼?带着种种疑问，我们来探究一下这种特殊类里函数的相关性侦.一、利用“二次函数”的性质研究“双勾函数”的性质1.“双勾函数”的定义我们把形如/（x）=x+E（A为常数.0j的函数称为“双勾函数”.因为函数X/（X）=+-（人为常数,JtO）在第一象限的图像如“，而该哈数为奇困数

2、，其图X像关于凝点成中心对称，故此而得名.2,类比“二次函数”与双勾函数”的图像3.类此“二次函数”的性质探究“双勾函数的性质“戈函中用性债0当“（.卜谕:轴的左侧.），地若K的增大而然冷心峭!怫渝），的若X的增大向增匕当=-层时.函数y有最小值但心X=嚼.：述时称轴的才曲，“/3时，在对称轴的左侧;Kir的增大ifii“6C、.当X=-时，函数y有坦大12）“双勾函数”性废的探究二次函数图像1.“双勾函数”图犀当x0时，在X=Jr左恻，,随箱X的增大而减小：在X=Jr的右恻,yRf1.tf.V的增大而增大：当X=J7时.函数），有最小值2.当XVO时，在X=-4的左蒯，随希X的增大而增大；在

3、X=-Jr的右IW,，随若X的增大而减小.当x=-4时.函数)，行最大值一2.综上知，函数/(*)在(To,-JFh川JT+动上单调递增，在-J.0)和(o,上单词递减.下面对“双勾函数”的性质作一证明.证明：定义法.设X.0wR,H.X2,则C、,/、ak(1-.t,X,-).Sk、/(x,)-(,)=xi+X,=j1.-1=(X1.-X,KI)X公演&X吊以卜我们假设何找到地战区间的分界点呢首先XHo.X=O就是一个分界点，另外我们用“相等分界法，&X=X=%,1-2=0可得到.r=J7.因此又找到两个分界点-JT,.这样就把f(x)的定义域分为(-8,-JT,-4.0),(0.JR,灰+

4、8)四个区间，再讨论它的IR调性.设ox.j4则芭-超0.01x,k.X1X2-0,即/(%)/(.马).TXy.V%5.C0在(0,Jr1.上单调通M.同理可得.在IJr,+8)1：单调递增：在(-8.-Ju.单调递增：在-,o)上单调递减.故函f(x)在(c,-1和JE,+8)上单词递增,在(-,)f(.|单调递性质启发：由函数八公二工+2仪的总调性及/(x)在其单调区间的然点处取值的X电劳，可作出闭数y=.r)的图像，反过来利用图像可形象地记忆该函数的总调性及有关性质.此性质是求解函数G值的强有力工具，特别是利用均值不等式而等号不成立时，更影显其单调性的强大功能.4.“二次函数*与“双勾

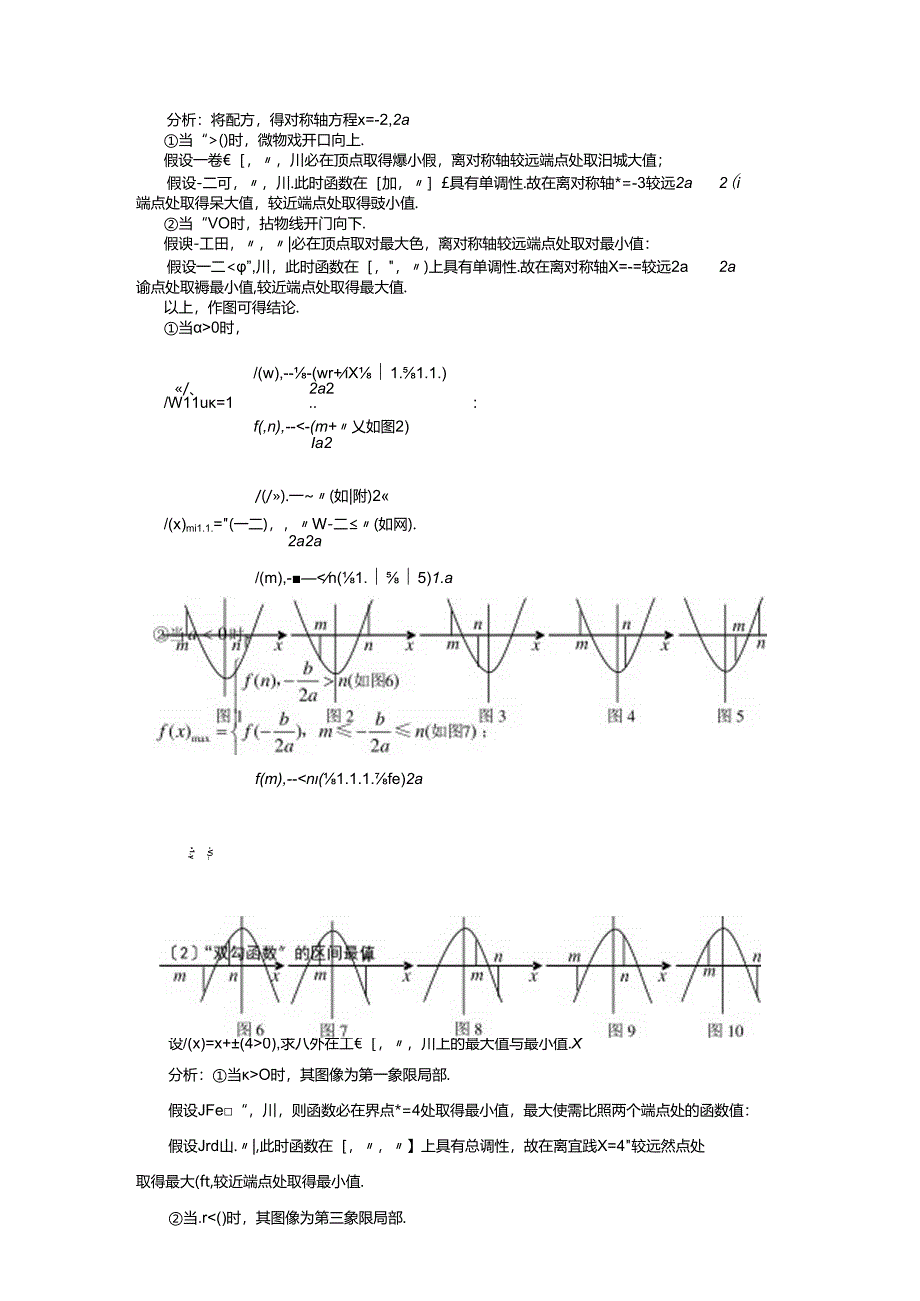
5、函数”在处理区间最值问题上的类比11)“二次函数的区间最值设/(x)=V+bv+()时，微物戏开口向上.假设一卷，川必在顶点取得爆小假，离对称轴较远端点处取汨城大值；假设-二可，川.此时函数在加，具有单调性.故在离对称轴*=-3较远2a2(i端点处取得呆大值，较近端点处取得豉小值.当“VO时，拈物线开门向下.假谀-工田，|必在顶点取对最大色，离对称轴较远端点处取对最小值：假设一二0时，/(w),-(wr+X1.1.1.)/、2a2/W11u=1.:f(,n),-(m+乂如图2)Ia2/(/).一(如|附)2/(x)mi1.1.=(一二)，W-二(如网).2a2a/(m),-n(1.5)1.af

6、(m),-0),求八外在工，川上的最大值与最小值.X分析：当O时，其图像为第一象限局部.假设JFe“，川，则函数必在界点*=4处取得最小值，最大使需比照两个端点处的函数值：假设Jrd山.|,此时函数在，】上具有总调性，故在离宜践X=4较远然点处取得最大(ft,较近端点处取得最小值.当.r()时，其图像为第三象限局部.假设-JEwm.1.1.,则函数必在界点x=-处取得最大伯，最小慎需比照两个端点处的函数值：超设-40，.此时函数在，”，川上具有单调性，故在离直筏X=-JT较远端点处取得损小值，较近端点处取得最大值.以上,作图可得结论.(2)每吨平均出厂价为16万元，年产房为多少吨时.可获得最大

7、利润并求出最大利润.分析：将向四归结为“双勾函数”同咫.利用“双勾函数”的性质，可使同Sfi轻松投好.解：(1)由题感可知，每吨平均本钱为S=上万元.XvV4fKK)14CXKX)即S=2=+J-30=(x+二)一30.因为函数在区间(O.2OO上为减函XIOXIOX数.在区间200.+)上为增函数.v14(NM)I44WRM)所以当x=200时，函数S=)=2+上一一30=-+上一)一30行最小值为-IOA-10ASAH=I200+胆&)-30=10(万元)，*小IO2(X)所以当年产量为200吨时，每吨的平均本钱最低,最低本饯为IO万元.(2)设年获得总利润为。万元,1则。=16x-)，=

8、16x-京+3()a-4(XX)=-(-23(+129().当x=230w(150.250),QM=I290,故当年产量为230吨时，可获得最大利润1290万元.评注：此题的关键是用年产用吨把毋吨平均本钱及利润表示出来，然后再求其最侦，在求解加值时我们要用到“双勾函数”的单调性，记住这个结论Ur以简化计修过程,函数的单词性除一些理论上的应用外,它还可以灵活疗效地糕决现实生活中与之相关的实际问趣.例2甲、乙两地相距Skm,汽车从甲地匀速行驶到乙地，速度不得超过CknVh,汽车每小时的运输本钱(以元为单位)，由可变局部和固定局部组成；可变局部与速度MknV1.D的平方成正比.比例系数为8.固定局部

9、为。元.(1)把全程运输本钱)，(元)表示为V(kmh)的函数.并指出这个函数的定义城.(2)为了使全程运怆本钱最小，汽车应以多大的速度行驶.分析：要计以全程的运输本钱)，=。+6，2)=(+6，)5(0v1)=(-+M5,又据题盍OvWc,故所求函数及其定义域分别为：VVy=s-(+bv),V(0,c,函数在(0.c上单词递破,所以当V=C时,全程运却本钱最小.评注：价应用题时，首先要训练读题能力，成功地完成时数学文字语言、符号语言、图形诺言的理解、承受和转换.继而对题中各元素的数技关系进展加工和提煤,分清主次.并建议数学镇型解决实际问8S.例312006安徼高考)函数f()在R上有定义，对

10、任意实数40和仔息实数.r,都fax)=afx.(I)证明，(O)=0：)1.(A0,1.其中A和力均为常数：Ax.xo.设geo=一+/(XXx0),讨论g(x)在(a+g)内/*)的单调性并求见价.分析：承接笫(II)问的给论，将问题归结为“双勾函数”的单调性与函数最磕的求和问题.证明：(I)令X=0,则/(O)=qf(O).u0,(0)=0.(II)令X=”，.a0.0,W1.(x2)=(x).假设x0时，/(x)=fcr(R),则/(F)=A,而(x)=x依=Jt,f(x2)=.rf(x),即/(x)=H成立.令X=-“，,*0./.0.y(-.r)=-v(x)假设XVO时，/(x)=

11、/u(/?),则/(一一)=一版2,而一01)=-*“1=-加二.f(-X2)=-(),即/(X)=近成立.()=kx.xO1.x,x0时,由“双勾函数”性质知在(0，,)上为战函数在U，+8)上为增函数.kk所以当X=4时，Iga)n,1,=2评注：数学而考试卷注重“考根基、考能力、考思r.所以熟悉数学化归的思矍，有意识地运用数学变换的方法去灵活解决有关的数学问麴,符仃利于强化在解决数学同包中的应变能力，有利于提高好淡数学问题的思维能力和技能、技巧.适当进展化归、转化能给人带来思维的闪光点，找到解决问题的突破口，是分析何时中思如:过程的主要组成局部.此题就是转化思想应用的一个典型，通过游化将本来抽象的问题归结到“双勾函数区间加值的求解.让我们有一种蔚然开朗的感觉.例4(2O(H广东高考)设计一幅宣传画，要求画面面枳为484Oan1.画面的宽与高的比为力(久=(z0),则Sa)=5000+352IO(r+r0).t函数S在(0,A1.上为减函数，在1器,+8)上为增函数,所以当r=S取最小值,此时=(1.),高:X=KScm,宽：=88=55cm.如果2G所以南数S在g,g上为增南数