专题02 等腰三角形的存在性问题(解析版).docx

《专题02 等腰三角形的存在性问题(解析版).docx》由会员分享，可在线阅读，更多相关《专题02 等腰三角形的存在性问题(解析版).docx（26页珍藏版）》请在第壹文秘上搜索。

1、专题二等腰三角形的存在性问题【考题研究】近几年各地的中考数学试题中，探索等三角形的存在性问题强艰出现，这类试题的知织Wk面较广，爆合性较强，意构思精巧，要求学生要有较高的分析向的能力和解决向JR的能力，这类问M符合课标对学生能力提育的聂求.【解题攻略】在讨论等腰三角形的存在性WJ时，一先分类.如果AABC是等腰三角形，那么存在AB=AC,BA-BC,CA=CB三种情况.娜等及三角形的存在性阿J三有几何法和代数法，把几何法和代数法相结合，可以使得解J又好又快.几何法TR分三步：分类、图、计算.骞些题目适合用几何法强？如果AABC的NA（的余弦值）是确定的，夹/A的两边AB和AC可以用含X的式子表

2、示出来，那么就用几何法.如图1,如果ABNAC,直控列方程I如图2,如果BAMBC,那么如图3,如果CA=CB,那么.代数法TR也分三步，罗并三边长，分类列方程，解方程并检验.如果三角形的三个角都是不现定的，面三个II点的坐标可以用含X的式子表示出来.那么根据两点间的距育公式，三边长的平方）就可以罗列出来.【解题类型及其思路】解围美S1.动态类S1.1.一动点类型问题；2.双动点或多动点类型向f1.!背景类型I1.几何BB形IMU2.平田亶角坐标系和几何图形IMI解息时几何法TR分三步，分类、图、计算代数法一般也分三步I罗列三边长，分类列方程，解方程并检验.如果ZSABC是等!三角形，那么存在

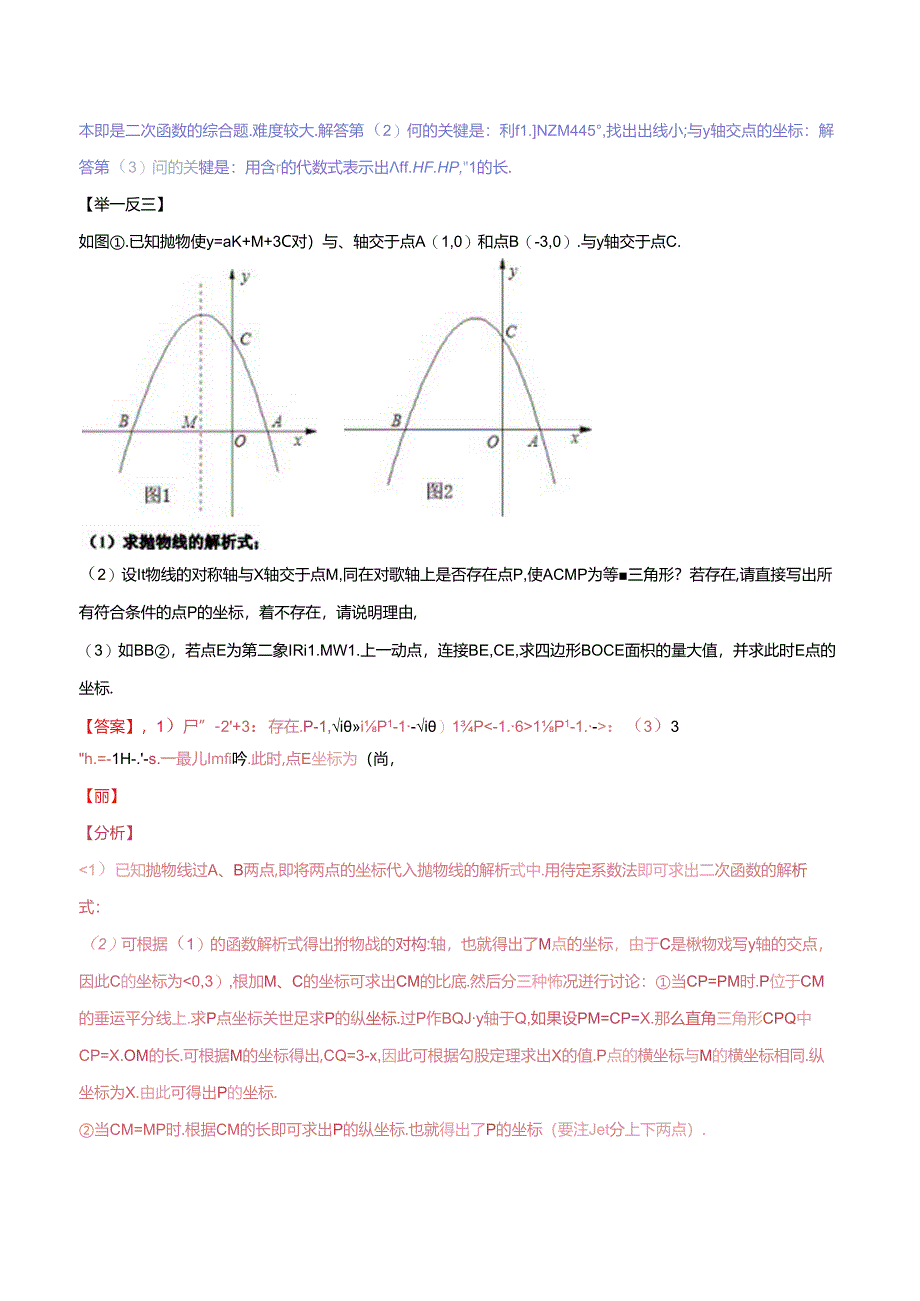
3、AB=AC,BA=BGCA=CB三种情况.已知长画等腰三角形用MH.已知底边等腰三角形用刻度尺重宣平分线解等三角形的存在性向Ji.有几何法和代数法,把几何法和代数法相结合，可以使得解愿又好又快.【典例指引】类型一【二次函数缥合题中根据条件判定三角形的形状】本即是二次函数的综合题.难度较大.解答第（2）何的关犍是：利f1.NZM445,找出出线小;与y轴交点的坐标：解答第（3）问的关犍是：用含r的代数式表示出ff.HF.HP,1的长.【举一反三】如图.已知抛物使y=aK+M+3C对）与、轴交于点A（1,0）和点B（-3,0）.与y轴交于点C.（2）设It物线的对称轴与X轴交于点M,同在对歌轴上是

4、否存在点P,使ACMP为等三角形？若存在,请直接写出所有符合条件的点P的坐标，着不存在，请说明理由,（3）如BB，若点E为第二象IRi1.MW1.上一动点，连接BE,CE,求四边形BOCE面枳的量大值，并求此时E点的坐标.【答案】，1）尸”-2+3：存在.P-1,iiP1-1-i）1P1P1-1.-：（3）3h.=-1H-.-s.一最儿Imfi吟.此时,点E坐标为（尚，【丽】【分析】1）已知抛物线过A、B两点,即将两点的坐标代入抛物线的解析式中.用待定系数法即可求出二次函数的解析式：（2）可根据（1）的函数解析式得出拊物战的对构:轴，也就得出了M点的坐标，由于C是楸物戏写y轴的交点，因此C的坐

5、标为BF=+3OF=-a,:“彩S=；陟EFOCEF).OF=-(+3)(-2-2+3)+-(-:-2+3+3)(一“)22一一+一222；.ia=1时,SWia悔ocJ,11；I.283Q1Sa=Ii.-a-2+3=1-3+3=244此修：,点E”标为(一T.V)OA=,OC=3,出勾股定理汨：AC=Jid,以点A为H心，AC的长为半fi什孤,交X轴于两点Di,Di,即为满足条此时它KJ的坐标分别为2(-Jid+,0),/(io,)八1.边时.？戈或ACm向平分线与X轴的交点&.即.笈件的点.i殳垂直AC的,CZN仙JP过ACIQ,.ZAOC=ZBOc=NPQC=90.NBPO=ZCPQ：.

6、ZACO=OD1P：.&CPQAcAOM)Fo.ODiCQCPOACOAC-PQ=警叫OD4OPOD1=PQio23二=谈四=4,6D1(-4.0)I)坐标为。(一1,0)或。式一+1,0),或4(加+1,0)或。1(-4Q)【名师点睹】此时是：次函数的综合理，考在待定系数法，最值问题的确定而将所求问题列出解析式并配方为顶点式，即可得到答案：3是图形中存在等腰.三角形问题，此类问应福分：种情况进行讨论,依次求出点的坐标.【举一反三】如图，已知抛物栽J=x2+bx+c的图象与X轴交于,1(2,O),I1.C-H,0)两点，与交于点C(0,-8).(I)求轴物线的解析式；(2)点/是直就下方抛物战

7、上的一点，当A8CF的面积大时，求出点尸的坐标：(3)在2)的条件下，是否存在这样的点。(O,m),使得AF。为等三角形？如果有，请直接耳出点。的坐标：如果没有，请说明理由.【答案】7)V-x-+3x-8：2)点尸的坐标是F(-4.-12)：(3)点Q行坐标为袁(0,-46)0.-4)或(0.0).【的】【分析】(I)将A,B.C的坐标代入函数尸=心+6+c即可；轴交8CJ-M求出仃线8C的解析式.设二(%y+3m-8),则NGn.8).再用台”,的代数式表示出8CF的I1.1.i枳.川函数的思想即可推出结论：3)此间要分8Q=6RQB=QF,F6=FQ=种情况迸行讨论,分别用句般定理可求出/

8、的值,进一步岂出点Q的坐标.【详解】1)将A(2.0),8(-8.0)C(0,-8)代入函数、=ar，+/w+c.4a+2b+c=0得，J4a-8b+c=00a+0b+c=-8Ia=2解得.2=3,C=-8衲物线解析式为-r+31.8：作&V轴交BC于N将5(80)代入y=k8,得.*=-I.)C=78,设F(阳，J病+3？8),则V(孙8).*5,wc=Samw*5f1=一FM82=AFN=4-m-8)-m23m-8)2=-2n2-I6/m=-2(r+4)-+32.当初=4时，A3C的面枳由鼓大值，此时广(4-12),，点尸的坐标是产4,-）2）：t2=4Jh：心(O.46.Qz(0,-46

9、I;如图2-2.图2-2当。8=0小时，出题意可列.SW=(m+12)-+4-.耨即，m=-4.；.Q(0.4)确,为什么？(3)连接CF、DF,请直接写出ACDF为答腰三角形时所有t的值.【答案】(I)y=-x+2x+3(2)点D为GC的中点时线段EF最长(3)1I：,3fj,(：为等腹.角形【呻】【分析】1)由于1.1.知帕物线与X釉交点砸标,则设交点式y=a(+1)(x-3).然后把C点坐标代入求出a即可得到她物城解析式：2)先利用待定系数法求出直观BC的解析式,再设EC,川+3，接着表示H1.D(O,3),F(bt,+2(+3),然后用t衣示出EF的长，再利用：次次数的性质定EF最大时

10、的I的低，从而判断巾D是否为OC的中点： 3)先由C.D(0.-t+3),F,-r+2*3)和利用两点间的距总公式衣示H1.CDCF1.,DF2,然后分类讨论：当CD=CF或FC=ID或DC=DF时得到关于t的方程,接看分别解关于I的方程即可.【佯解】 1)设抛物战的解析式为y=a(x+1.)(x-3).把C(Q,3)代入得a1.(-3)=3.MMBa=I.所以拗物线解析式为y=-x+1.)(x-3),即y=-x,2x+3: 2)他猜把正确.理由如下：设直线BC的解析式为y-mxn.JCCIJnj3rvP践K的解析式为3m+n=0(n=3设E(1.7+3)，则D(0.-t+3F(t-1+21+

11、3).所以EF=-I+2i+3-(t+3)=-t1+3t=.当。号时，EF最大,JR大值欧,此时D点坐标为(0,三),所以点D为OC的中点时,线段EF最长：(3) VC(0.3).D(0.-t3),F(t,-t*+2t*3),.C)-1.+3-3)I,(2t3-3:=t+21.)Z.Di;：-t:+21.+3+t-3)-+3t)*.当Q)=CF时，即t*=t1+:,解得t=0,1尸2：当FC=FD,即：.(-t+2t)=t+:.蚱得t=0.：当DC=DF时，即tx=t1+(-f+3t2.解得t=0,t=3:疗匕所述,节1=2或!或3时,ACDF为等腰角形.【新题训练】I.如图，在平面直角坐标系

12、中,已知点M-2,-4),直线=-2与、轴相交于点B,连接OA,It物线J=-x从点O沿OA方向平移，与宣线X=-2交于点P，顶点M到点时停止移动.Q)线段OA所在直钱的函数解析式是t(2)设平移后抛初线的!点、1的横坐标为m,问：当m为何值时，战段PA量长？井求出此时PA的长.(3)若平移后撤物线交y轴于点Q,是否存在点Q使得AoMQ为三角形？若存在，请求出点Q的坐标I若不存在，请说明理由.【答案】y=2x：U；1-In=I1.1.PA的值融大,M的最大玳为1：m存/1.,5()-j.ADE的血枳取得被大：33【答案】1；，K函数的解析人为y=-%-3+6：2;+C=O.c=6解得:所以：次函数的解析式为；尸-2/-之工+6：422)iA(-4.0),E(0,2),可求AE所4F线解析式为过点。作ZUx轴，交4于点儿交A轴干点G,过点E作EOR乖足为“，如