 大学物理非线性振动.ppt
大学物理非线性振动.ppt
《大学物理非线性振动.ppt》由会员分享,可在线阅读,更多相关《大学物理非线性振动.ppt(14页珍藏版)》请在第壹文秘上搜索。
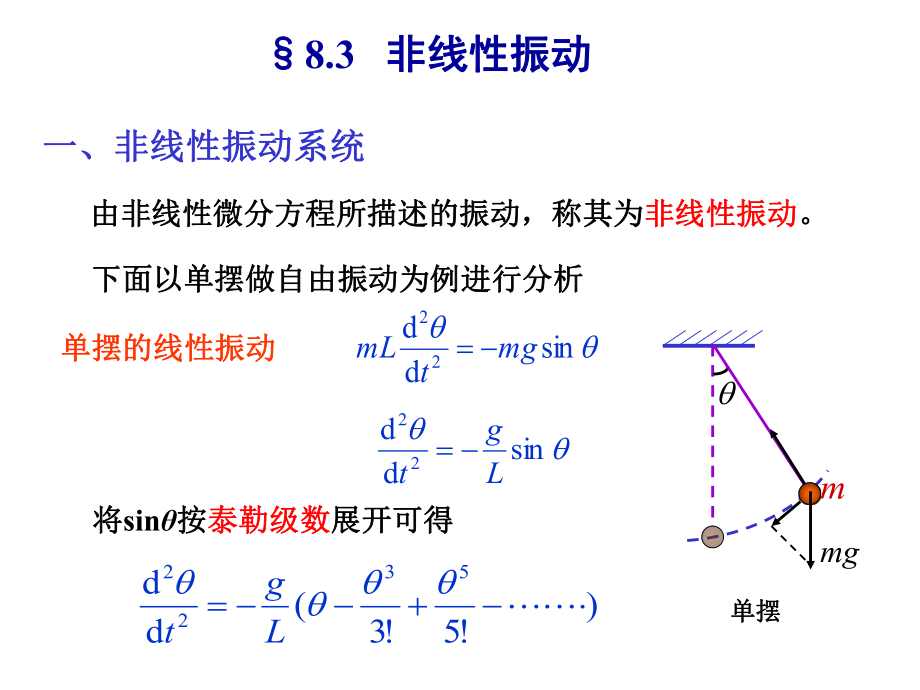
1、8.3 非线性振动非线性振动 一、非线性振动系统一、非线性振动系统由非线性微分方程所描述的振动由非线性微分方程所描述的振动,称其为,称其为非线性振动非线性振动。下面以单摆做自由振动为例进行分析下面以单摆做自由振动为例进行分析单摆的线性振动单摆的线性振动sindd22mgtmLsindd22Lgt将将sin按按泰勒级数泰勒级数展开可得展开可得mmg)! 5! 3(dd5322Lgt单摆单摆很小时,很小时,3 3以上可忽略不计,以上可忽略不计,同时令同时令2=g/L可得可得222ddt由上式可知,由上式可知,小角度小角度下单摆的运动是简谐振动下单摆的运动是简谐振动,其其周期周期为为gLT2单摆的非
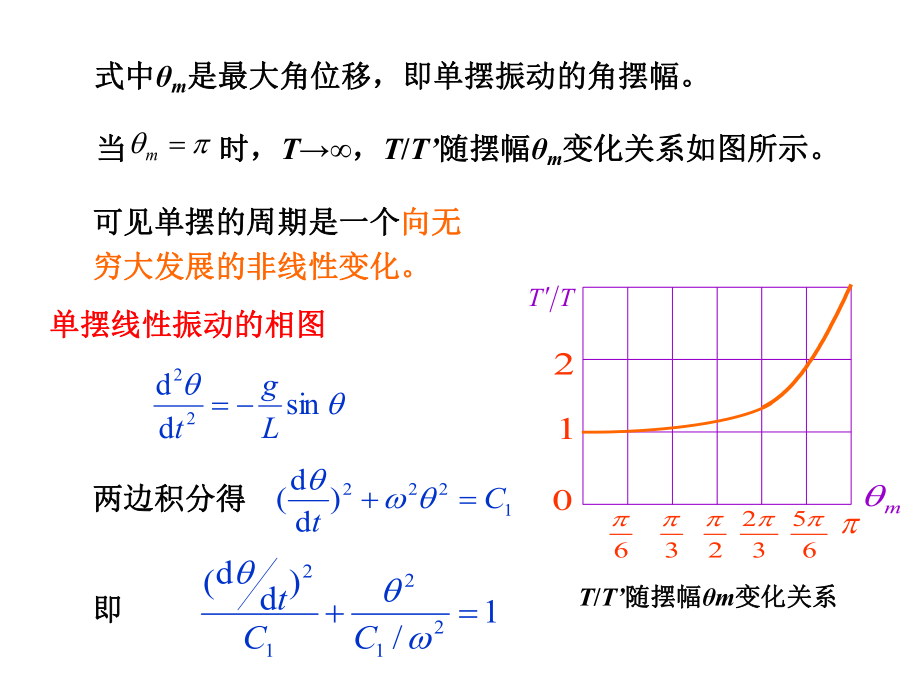
2、线性振动单摆的非线性振动随着随着的增大,摆球的运动方程为一个非线性微分方程。的增大,摆球的运动方程为一个非线性微分方程。可以证明单摆的周期变为可以证明单摆的周期变为)2sin6492sin411 (242mmglT式中式中m是最大角位移,即单摆振动的角摆幅。是最大角位移,即单摆振动的角摆幅。当当 时时,T,T/T随摆幅随摆幅m变化变化关系如图所示。关系如图所示。m可见可见单摆的周期是一个单摆的周期是一个向无向无穷大发展的非线性变化。穷大发展的非线性变化。两边积分得两边积分得1222)dd(Ct单摆线性振动的相图单摆线性振动的相图sindd22Lgt6323265012mTT1/)dd(2121
3、2CCt即即T/T随摆幅随摆幅m变化关系变化关系可见,线性振动的相轨迹为可见,线性振动的相轨迹为椭圆椭圆, ,中心点是稳定的中心点是稳定的奇点奇点. .初始条件确定后,单摆运动过程就初始条件确定后,单摆运动过程就对应于其中一个椭圆,对应于其中一个椭圆,单摆的运动单摆的运动是一系列的同周期运动,且运动状是一系列的同周期运动,且运动状态完全确定。态完全确定。单摆非线性振动的相图单摆非线性振动的相图如果对摆角不加限制,微分方程变成非线性微分方程,对方如果对摆角不加限制,微分方程变成非线性微分方程,对方程两边积分可得程两边积分可得tddo22cos)dd(21CLgt单摆无阻尼线性振动的相图单摆无阻尼
4、线性振动的相图当当t=0时,时,=00ddt02cos/LgC)cos(cos2dd0Lgt可见,其相图不再是一椭圆,可见,其相图不再是一椭圆,相轨迹两端凸出略呈尖角状,相轨迹两端凸出略呈尖角状,但仍是封闭曲线,但仍是封闭曲线,表示运动表示运动仍是周期性往复摆动仍是周期性往复摆动。当摆幅增大当摆幅增大到时,相迹线上出现了两个分支点,我们称到时,相迹线上出现了两个分支点,我们称之为之为鞍点鞍点, ,如上图如上图. .tddo单摆无阻尼非线性振动的相图单摆无阻尼非线性振动的相图鞍点鞍点和中心点一样也是一个和中心点一样也是一个奇点奇点,但是在鞍点上但是在鞍点上 m0ddt0dd22t说明说明鞍点鞍点
5、是不稳定的平衡点,是不稳定的平衡点,因为与之相连的四条相轨迹中因为与之相连的四条相轨迹中两条指向它,两条背离它,而两条指向它,两条背离它,而附近相轨迹呈双曲线状附近相轨迹呈双曲线状tddopEo从势能曲线和相图上可知从势能曲线和相图上可知处势能最大,处势能最大,势能曲线、相图、鞍点势能曲线、相图、鞍点双曲点的存在,预示着混沌运动的可能双曲点的存在,预示着混沌运动的可能假定存在阻尼和驱动力,让摆作受迫振动这样一来,假定存在阻尼和驱动力,让摆作受迫振动这样一来,双曲点就成了双曲点就成了敏感区敏感区能量稍大,单摆就会越过势垒的能量稍大,单摆就会越过势垒的顶峰,跨到它的另一侧;能量稍小,则为势垒所阻,
6、滑顶峰,跨到它的另一侧;能量稍小,则为势垒所阻,滑回原来的一侧单摆向回摆动。回原来的一侧单摆向回摆动。二、二、非线性振动系统的混沌行为非线性振动系统的混沌行为仍以单摆为例仍以单摆为例, 前面已经讨论过它的自由振动前面已经讨论过它的自由振动,下面分析下面分析其阻尼振动和受迫振动其阻尼振动和受迫振动有阻尼、无策动力的振动有阻尼、无策动力的振动小摆幅时运动方程为小摆幅时运动方程为小摆幅时小摆幅时,按阻尼的大小其运动状态可分为按阻尼的大小其运动状态可分为过阻尼过阻尼、临界临界阻尼阻尼、和、和阻尼振动阻尼振动.从相图可知从相图可知,无论单摆从什么初始状态无论单摆从什么初始状态出发出发,最后都要静下来最后

- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 大学物理 非线性 振动
 第壹文秘所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
第壹文秘所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。


 重点工作绩效评估自评表.docx
重点工作绩效评估自评表.docx
