电容电容器(大学物理)..ppt

《电容电容器(大学物理)..ppt》由会员分享，可在线阅读，更多相关《电容电容器(大学物理)..ppt（21页珍藏版）》请在第壹文秘上搜索。

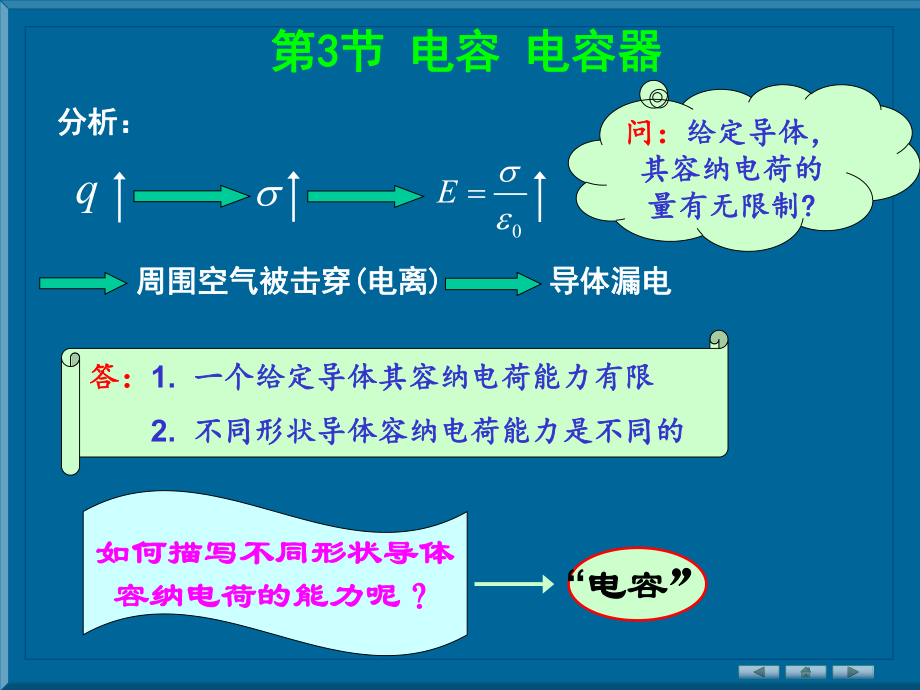
1、第第3 3节节 电容电容 电容器电容器问：问：给定导体，给定导体，其容纳电荷的其容纳电荷的量有无限制量有无限制? ?导体漏电导体漏电周围空气被击穿周围空气被击穿( (电离电离) )0Eq如何描写不同形状导体如何描写不同形状导体容纳电荷的能力呢？容纳电荷的能力呢？“电容电容”答：答：1. 一个给定导体其容纳电荷能力有限一个给定导体其容纳电荷能力有限 2. 不同形状导体容纳电荷能力是不同的不同形状导体容纳电荷能力是不同的分析：分析：一、孤立导体的电容一、孤立导体的电容 CUq：电容，：电容， SI：C/V=F（法拉）（法拉） 当当U=1v时，导体上所容纳的电荷即为时，导体上所容纳的电荷即为电容电容

2、 比值：比值：实验指出：实验指出：当孤立导体带电量增加，电势也随之增加当孤立导体带电量增加，电势也随之增加 但电量和电势的比值始终恒定但电量和电势的比值始终恒定说明该比值反映了说明该比值反映了导体的电学自然属性导体的电学自然属性qUqU注：孤立导体的电容既不依赖于所带电量注：孤立导体的电容既不依赖于所带电量也不依赖于电势也不依赖于电势例：孤立导体球例：孤立导体球RqU04解：解： RC04地3121064001085. 844100 . 7= = ORqUUqC0R04rORqRqUr04004rrqCRCU 注：注：电容电容与与导体是否带电无关导体是否带电无关 与导体与导体几何因素几何因素和

3、和周围介质周围介质有关有关（F F） rAB二、电容器及电容二、电容器及电容 AUBUqq( (正极板正极板) ) ( (负极板负极板) ) ABABUUU由彼此绝缘、相距很由彼此绝缘、相距很近的两导体构成近的两导体构成实验与理论证明：实验与理论证明： ABqU常量常量 CUqAB注意：注意：C 取决于电容器的取决于电容器的形状、大小、相对位置形状、大小、相对位置及其间及其间介介质质 ：电容：电容 AB三、几种典型的电容器三、几种典型的电容器 1 1、平行板电容器、平行板电容器 SSdDSDS= = = = 0rDE ，SQErr00ABUEdABQCU， dSC00QQSrdS00CdSUQ

4、CrrAB 1 1、加入介质是提高电容的一种方法、加入介质是提高电容的一种方法 2 2、电容器上通常标注的、电容器上通常标注的2 2个数据，个数据，egeg：5PF5PF，100v100v耐压限度耐压限度2 2、球形电容器、球形电容器SSdDQrD24= = 24 rQD= = 0rE ，204rQEr21RRUE dldrrQRRr21204)11(4210RRQr210124)(RRRRQr0122104CRRRRUQCrr， 1221004RRRRC讨论：讨论：1R固定，固定， 2R104RCr， rQQrO2R1R=3 3、柱形电容器、柱形电容器 12(,)lR RSSdDQrlD2=

5、 = rlQD2Er0= = rlQEr0221RRl dEUdrrlQRRr2102120ln2RRlQr= = = = 0120)/ln(2CRRlUQCrr， )/ln(21200RRlCrQQr1R2Rl回顾：回顾：CUq：电容，：电容， SI：C/V=F（法拉）（法拉） 比值：比值：1、孤立导体的电容：、孤立导体的电容： qUqU孤立导体的电容与导体孤立导体的电容与导体几何因素几何因素和和周围介质周围介质有关有关2、电容器的电容：、电容器的电容： rABAUBUqq( (正极板正极板) ) ( (负极板负极板) ) CUqAB：电容：电容 电容器电容电容器电容取决于电容器的取决于电容

6、器的形状、大小、相对位置形状、大小、相对位置及其间及其间介质介质 例：求电容。例：求电容。 解：解： 031EEErEE02， 00ESQ0= = )(12tdEtEU)(00tdEtEr)(0tdtSQr= = = = rrrtdtStdtSUQC)()/(00rEE/0不成立的情况：不成立的情况： 101/rEE202/rEErEE0102EE 101rEE202rEEQQQQQQdIIIISt,rII r2R例：导体球，外包一层电介质例：导体球，外包一层电介质求：电容求：电容 解：解： 22021201440RrrQRrRrQRrErU= = 1cosRdlE21204RRrdrrQ=

7、= = = 2204RdrrQ+ + )11(4210RRQr2014RQ+ + 1)11(142210RRRQr= = UQC 22101)11(14RRRr1122104RRRRRrr= = = = QO1R第第4 4节节 电场的能量电场的能量当当A已已带有电荷带有电荷 ，具有电势为，具有电势为 u 时，时，quQqdq一、带电体系的能量一、带电体系的能量该系统所具有的电势能该系统所具有的电势能把各电荷元从无限远离的状态把各电荷元从无限远离的状态聚集成该带电体系的过程中，外力所做的功聚集成该带电体系的过程中，外力所做的功A外力不做功外力不做功 外力开始克服静电力做功外力开始克服静电力做功

8、再把再把 dq 从从A， 外力克服静电力做功外力克服静电力做功dA 随着随着q ，u ，第二个第二个dq从从 A， =udq= =第一个第一个dq从从 A， 搬运同样多的搬运同样多的dq，外力做的功，外力做的功dAdq电势能的增量电势能的增量在在A带电的全部过程中，带电的全部过程中，外力做功为变力做功外力做功为变力做功 此功全部转化为此功全部转化为A这个这个带电体系的能量带电体系的能量0QWudq例：孤立导体球的静电能例：孤立导体球的静电能解：解： Rqu04，dqRqudq04QdqquW0)(QdqRq004RQ028= = = = qdqQORuQqdqAAdAudq二、电容器的能量二、

9、电容器的能量 已搬运的电荷已搬运的电荷q电势差电势差CquAB/搬运搬运dq过程外力克服电场力过程外力克服电场力 作功作功dqudAAB外力克服电场力作功的总和：外力克服电场力作功的总和：电容器的能量电容器的能量 QABdquW0QdqCq0CQ22ABQCU= = = = ， CQW2212ABQU212ABCU= = = = 电容器储能公式电容器储能公式 QQdqAqCqB注注: 任意形状的电容器，其能量均为上式任意形状的电容器，其能量均为上式三、电场的能量三、电场的能量 dSCr0ABUEdCQW22212ABCU20)(21EddSrVESdErr20202121= = = = = =

10、 能量分布在电场中能量分布在电场中 电场电场是能量的携带者是能量的携带者 电场能量密度电场能量密度 dVdWw dVdWw 2012rE ， 2Ew SQQdrdVdWE= = 适用任意适用任意电场电场1122DED E带电系统的能量带电系统的能量OR均匀电场，均匀电场， wVW 非均匀电场，非均匀电场， VwdVdWWVrdVE2021= = 例：孤立导体球电场的能量例：孤立导体球电场的能量解：解： 2004rREQrRr22024001232rrRwEQrRr RrRrVwdVwdVwdVWdrrrQR24022432RQ028= = = = drdrrdV24rQ计算计算带电系统静电能带

11、电系统静电能或或电场能量电场能量的方法：的方法：(1)(1)电容器，电容器， CQW22(2)已知已知E， VwdVWVrdVE2021= = (3)搬运方法，搬运方法， 0QWudq例：两个相同例：两个相同R和和Q的球面和球体，带电均匀，哪个电能大？的球面和球体，带电均匀，哪个电能大？1W2W例：平板电容器各参量（真空中）在充入介质时有何变化？例：平板电容器各参量（真空中）在充入介质时有何变化？分析两种条件下，为何分析两种条件下，为何E会出现不同的结果？会出现不同的结果？0rC0rC0r 00rE0E0U0tU0D0rD0rW0rW当当Q不变时不变时当当U不变时不变时 真空真空 0C00E0

12、U0D0W22QWC22CUW 1. 当当Q不变时，介质被极化，消耗电能，不变时，介质被极化，消耗电能，0rEE2. 当当U不变时，介质被极化，消耗电能，不变时，介质被极化，消耗电能，但电源会提供能量以保持但电源会提供能量以保持U不变，所以不变，所以 不变不变UEd解之得：解之得：U相同：相同：Q守恒：守恒： 解：解： 212121rQQQQCCCC例：两相同的电容器，充电后与电源断开，然后在例：两相同的电容器，充电后与电源断开，然后在1中充入介质，中充入介质，问问 如何变化？如何变化？222,Q UW2112QQQ1211rrrQQQQ2Q22QUC2222QWC假设原来各带电假设原来各带电

13、2Qr解之得：解之得：U不变：不变：Q相等：相等： 解：解： 12UUU例：两相同的电容器，串联与电源相接，然后在例：两相同的电容器，串联与电源相接，然后在1中充入介质，中充入介质，问问 如何变化？如何变化？222,Q UW112212rCUC UCUCU12111rrrUUUU2U2221rrQC UCU22222222QQWCC21U12CUr等值电容等值电容等值电容等值电容niiCC（1）提高电容器电容量）提高电容器电容量并联并联12QQCUUU11niiCC（2）提高电容器耐压能力）提高电容器耐压能力串联串联耐压能力不变耐压能力不变电容提高电容提高耐压能力提高耐压能力提高电容减小电容减小电容器的串并联：电容器的串并联：2C1C2C1CU12QQQCUU1212CUC UCCU1212111QQQCCCC四、电荷与外电场的相互作用四、电荷与外电场的相互作用外电场，外电场， 外E、外U受力受力 电势能电势能 点电荷点电荷 外EqF0外UqW0点电荷系点电荷系 iiEqF外iiUqW外带电体带电体 dqEF外dqUW外研 究 对 象 注意：注意： 外E、外U是外电场的场强和电势是外电场的场强和电势 不包括研究对象自身产生的电场和电势不包括研究对象自身产生的电场和电势QQSA A B B 例：两块导体板的例：两块导体板的 相互作用力相互作用力 解：解：SQQF02022