高等代数知识点总结.ppt

《高等代数知识点总结.ppt》由会员分享，可在线阅读，更多相关《高等代数知识点总结.ppt（41页珍藏版）》请在第壹文秘上搜索。

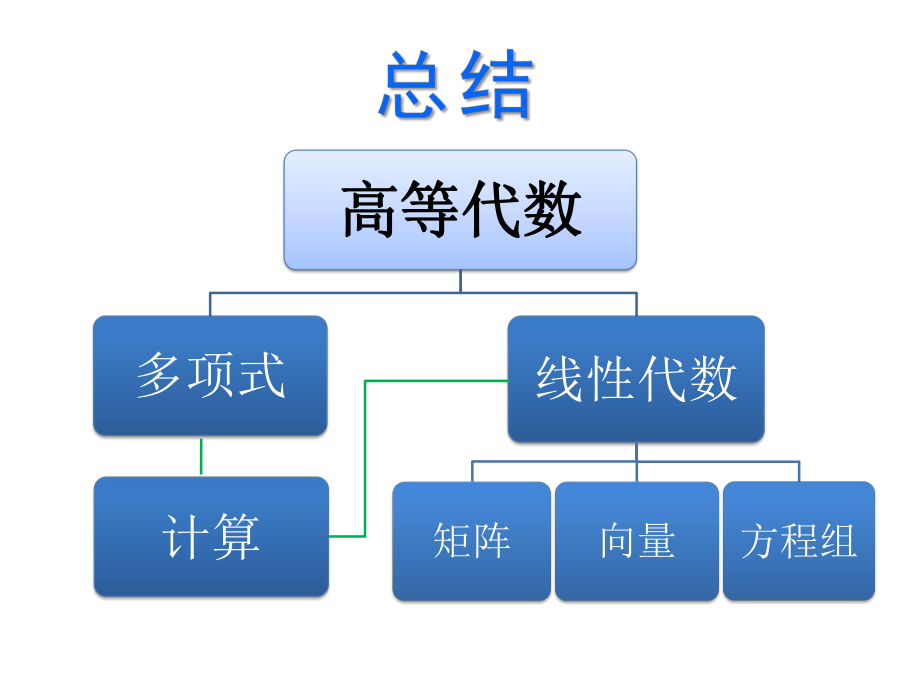
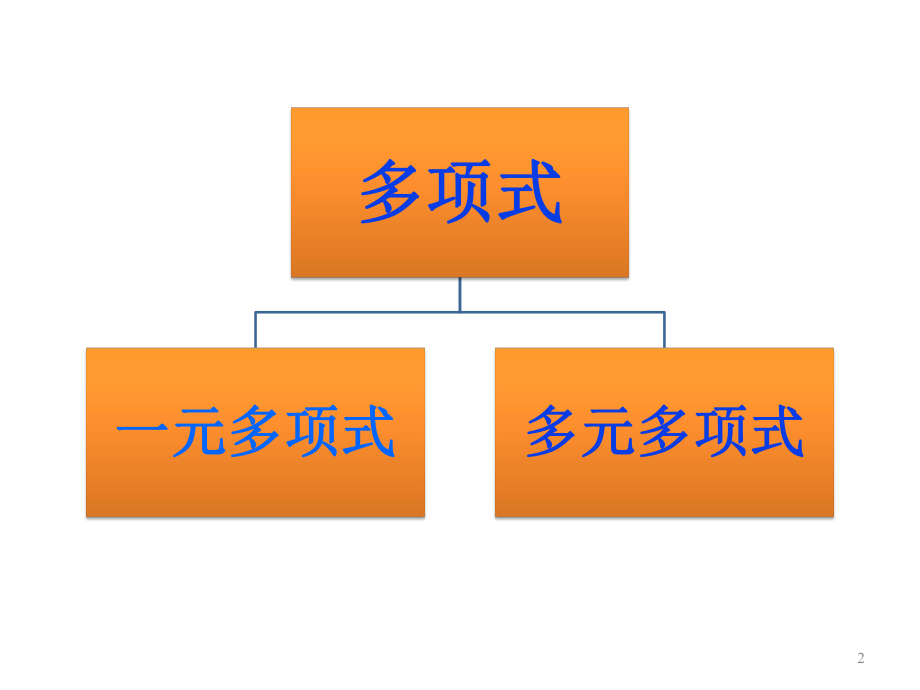
1、高等代数高等代数多项式线性代数矩阵向量方程组计算多项式多项式一元多项式一元多项式多元多项式多元多项式2 基本概念基本概念：次数：最基本的概念和工具整除：多项式之间最基本的关系带余除法：最基本的算法，判断整除.最大公因式：描述多项式之间关系的复杂程度互素：多项式之间关系最简单的情形既约多项式：最基本的多项式根：最重要的概念和工具一元多项式一元多项式3 重要结论重要结论： 带余除法定理对于任意多项式f(x)和非零多项式g(x)，有唯一的q(x)和r(x)使得f(x)=g(x)q(x)+r(x)，r(x)=0或degr(x)degg(x). 最大公因式的存在和表示定理 任意两个不全为0的多项式都有最

2、大公因式，且对于任意的最大公因式d(x)都有u(x)和v(x)使得d(x)=f(x)u(x)+g(x)v(x) 互素f(x)和g(x)互素有u(x)和v(x)使得f(x)u(x)+g(x)v(x)=1.4 因式分解唯一定理 次数大于1的多项式都可分解成有限个既约多项式之积，且不计因子次序和常数因子倍时，分解唯一. 标准分解定理 每个次数大于1的多项式f都有如下的标准分解其中a是非零常数, p1,pt, 是互不相同的首一既约多项式, n1,nt是正整数. 进一步,a, p1,pt,n1,nt由f唯一确定.11tnntfapp 重因式 f无重因式当且仅当f与其导式互素.5代数学基本定理：下列陈述等

3、价，1. 复数域上次数1的多项式总有根2. 复数域上的n次多项式恰有n个根3. 复数域上的既约多项式恰为一次式4. 复数域上次数1的多项式可分解成一次式之积.5. 实数域上的次数1的既约多项式只有无实根的二次式6. 实数域上次数1的多项式可分解成一次式和二次式之积6 实数域上的标准分解定理 在实数域上，每个次数大于1的多项式f都有如下的标准分解其中a是f的常数项, x1,xt 是f全不互不相同的根, p1,pt是互异、首一、无实根的二次式. 复数域上的标准分解定理 在复数域上，每个次数大于1的多项式f都有如下的标准分解其中a是f的常数项, x1,xt 是f全部互不相同的根, n1,nt分别是这

4、些根的重数.11()()tnntfa xxxx1111()()stmnmnstfa xxxxpp7 多项式作为函数： 两个多项式相等(即对应系数相同)它们作为函数相等(即在每点的函数值相等)它们在k+1个点的函数值相等，这里k是它们次数的最大者. 设f(x)anxn+.+a1x+a0，若f(x)在n+1个点的函数值为0，则f(x)恒等于0.8 Eisenstein判别法： 设 是整系数多项式，若有素数p使得 则f(x)是有理数域上的既约多项式. 有理根：有理根的分母整除首项系数，分子整除常有理根的分母整除首项系数，分子整除常数项数项10( )nnf xa xa xa2100,|,.,|nnp

5、app ap aa9l 重要结论重要结论 命题1.8.1 若多项式的值全为0，则该多项式必为0. 命题1.8.2 每个n次多项式f均可唯一地表示成齐次多项式之和 ，fn0，且其中fi是0或i次齐次多项式，0in，fi称为f的i次齐次分量.l 基本概念基本概念：次数、齐次分量、字典序、首项、对称多项式多元多项式多元多项式01nffff对称多项式基本定理 每个对称多项式，都可唯一地表示成初等对称多项式的多项式.10矩阵矩阵运算运算行列式行列式初等变换初等变换和标准形和标准形特殊矩阵特殊矩阵11运算及其关系运算及其关系转置转置取逆取逆伴随伴随行列式行列式秩数秩数加加法法(A+B)T=AT+BTr(A

6、+B)r(A)+r(B)数数乘乘(kA)T= k AT(kA) 1= k 1A 1 (kA)*= kn 1A*|kA|=kn|A|r(kA)=r(A) (k0)乘乘 法法(AB)T= BT AT(AB) 1= B 1 A 1(AB)*= B*A*|AB|=|A|B|r(A)+r(B)-nr(AB)r(A), r(B)转转置置(AT)T=A(AT) 1=(A 1)T(AT)*=(A*)T|AT|=|A|r(AT)=r(A)取取逆逆(A 1) 1=A(A 1)*(A*) 1|A 1|=|A| 1伴伴随随(A*)*=|A|n 2A*|A*|=|A|n 1 n, 若r(A)=n r(A*)= 1, 若

7、r(A)=n-1 0, 若r(A)n-1其其它它A-1=|A|-1A*AA*=A*A=|A|E当当A可逆时，可逆时，A*|A|A 1定义定义性质性质若P,Q可逆，则r(A)=r(PA)=r(AQ) =r(PAQ)12转置转置取逆取逆伴随伴随加法(A+B)T=AT+BT数乘(kA)T= k AT(kA) 1= k 1A 1 (kA)*= kn 1A*乘法(AB)T= BT AT(AB) 1= B 1 A 1(AB)*= B*A*转置(AT)T=A(AT) 1=(A 1)T(AT)*=(A*)T取逆(A 1) 1=A(A 1)*(A*) 1伴随(A*)*=|A|n 2A*其它A-1=|A|-1A*

8、AA*=A*A=|A|I当当A可逆时，可逆时，A*|A|A 113行列式行列式秩数秩数加法r(A+B)r(A)+r(B)数乘|kA|=kn|A|r(kA)=r(A) (k0)乘法|AB|=|A|B|r(A)+r(B)-nr(AB)r(A), r(B)转置|AT|=|A|r(AT)=r(A)取逆|A 1|=|A| 1伴随|A*|=|A|n 1 n, 若若r(A)=n r(A*)= 1, 若若r(A)=n 1 0, 若若r(A)n 1 其它定义定义性质性质若P, Q可逆，则r(A)=r(PA)=r(AQ) =r(PAQ)14性质公式备注转置不变性|AT| = |A|行列地位平等反交换性|.| =

9、|.|换法变换交错性|.| = 0齐性|.k.| = k|.|倍法变换统称线性加性|.+.| = |.| + |.|倍加不变性|.+k.| = |.|消法变换按第k行第k列展开 |aij| = ak1Ak1+aknAkn = a1kA1k+ankAnkaj1Ak1+ajnAkn = a1jA1k+anjAnk =jk|aij| Laplace定理分块三角矩阵的行列式Cauchy-Binet 公式Vandermonde行列式定义 性质；11111|kkkAAjjkkiiiiAjjjj式代余式111-|-mmUViimiiUVii式式1511111|kkkAAjjkkiiiiAjjjj式代余式La

10、place定理 (按第i1,.,ik行展开)0*|*0AAABBB0*( 1)|*0mnAAABBB ；分块三角形行列式16111-|-mmUViimiiUVii式式Cauchy-Binet公式公式 设U是mn矩阵, V是nm矩阵, mn, 则171222212111111111()0,.,j nnnjiinnnnnxxxVxxxxxxxxVxx 互不相同18初等变换初等变换行变换行变换列变换列变换换法变换换法变换倍法变换倍法变换消法变换消法变换101101 1111c1111c对单位矩阵做一次初等变换对单位矩阵做一次初等变换对对A A做一次做一次行行变换变换 = = 用相应的初等矩阵用相应的

11、初等矩阵左左乘以乘以A A对对A A做一次做一次列列变换变换 = = 用相应的初等矩阵用相应的初等矩阵右右乘以乘以A A19 对于对于mn矩阵矩阵A，B下列条件等价下列条件等价1. A B，即，即A可由初等变换化成可由初等变换化成B2. 有可逆矩阵有可逆矩阵P,Q使得使得PAQ=B3. 秩秩A=秩秩B4. A，B的标准型相同的标准型相同 A,B行等价行等价有可逆矩阵有可逆矩阵P使得使得A=PB 每个矩阵都行等价于唯一一个每个矩阵都行等价于唯一一个RREF矩阵矩阵 A,B等价等价有可逆矩阵有可逆矩阵P,Q使得使得A=PBQ 每个每个秩数为秩数为r的矩阵都等价于的矩阵都等价于000rI矩阵等价矩阵

12、等价20可逆矩阵vs列满秩矩阵对于对于n n阶矩阵阶矩阵A,A,下列条件等价下列条件等价1.1. A A是可逆矩阵是可逆矩阵2.2. |A|A| 0 03.3. 秩秩A=nA=n4.4. 有有B B使得使得AB=IAB=I或或BA=IBA=I5.5. A A是有限个初等矩阵之积是有限个初等矩阵之积6.6. A(A(行或列行或列) )等价于等价于I I7.7. A A的列的列( (行行) )向量组线性无关向量组线性无关8.8. 方程组方程组Ax=0Ax=0没有非零解没有非零解9.9. 对任意对任意b,Ax=bb,Ax=b总有解总有解10.10.对某个对某个b,Ax=bb,Ax=b有唯一解有唯一解

13、11.11.A A是可消去的是可消去的( (即由即由AB=ACAB=AC或或BA=CABA=CA恒可得恒可得B=C)B=C)对于对于m mr r矩阵矩阵G,G,下列条件等价下列条件等价1.1. G G是列满秩矩阵是列满秩矩阵, ,2.2. G G有一个有一个r r阶的非零子式阶的非零子式3.3. 秩秩G=G=列数列数4.4. G G有左逆有左逆, ,即有即有K K使得使得KG=IKG=I5.5. 有矩阵有矩阵H H使得使得(G, H)(G, H)可逆可逆6.6. G G行等价于行等价于7.7. G G的列向量组线性无关的列向量组线性无关8.8. 方程组方程组Gx=0Gx=0没有非零解没有非零解

14、9.9. 对任意对任意b,b,若若Gx=bGx=b有解有解则唯一则唯一10.10.对某个对某个b,Gx=bb,Gx=b有唯一解有唯一解11.11.G G是左可消去的是左可消去的( (即由即由GB=GCGB=GC恒可得恒可得B=C)B=C)0rI21设A的秩数为r, 则A有如下分解1. ,其中P,Q为可逆矩阵 2. A=PE,其中P可逆,E是秩数为r的RREF3. A=GH,其中G列满秩,H行满秩,且秩数都是r (满秩分解)矩阵分解矩阵分解00 0rAPQI221.分块矩阵的初等变换和Schur公式 把初等变换和初等矩阵的思想用到分块矩阵 Schur公式 设A可逆 两种常用方法两种常用方法111

15、1111IOABA BC DCAIO D CA BAOA BIA BC DOIB D CA BIOAOA BIA BC DOICAIO D CA B适用例子: 习题3.7.5; 3.7.911:232.正则化方法 证明当A可逆时结论成立 考虑xI+A,有无穷多个x使得该矩阵可逆 将要证明的结论归结为多项式的相等 若两个多项式在无穷多个点处的值相同,则这两个多项式在任意点的值相等,特别地,取x=0.适用例子: 习题3.6.4; 3.7.7; 3.7.11:24特殊矩阵三角 正规 可逆对合 Hermite 反Hermite 酉矩阵 幂等 幂零 对称 反对称 正交 对角 纯量 25向量线性关系线性相

16、关线性无关线性表示等价极大无关组秩数26线性表示： 列向量组1,.,r可由1,.,s线性表示当且仅当有矩阵C使得(1,.,r)=(1,.,s)C. 进一步，C的第k列恰为k的表示系数 线性表示有传递性 被表示者的秩数表示者的秩数向量组等价：对于向量组S，T，下列条件等价1. S和T等价，即S,T可以互相表示2. S,T的极大无关组等价3. S,T的秩数相等，且其中之一可由另一表示27线性相关与线性表示： 1,.,r线性相关当且仅当其中之一可由其余的线性表示 若,1,.,r线性相关,而1,.,r线性无关,则可由1,.,r线性表示,且表法唯一线性无关：对于向量组1,.,r下列条件等价 1,.,r线性无关 当c1,.,cr不全为0时，必有c11+.+crr0 当c11+.+crr0时，必有c1.cr0 1,.,r的秩数等于r (1,.,r)是列满秩矩阵28极大无关组与秩数：1. 1,.,rS是S的一个极大无关组当且仅当 1,.,r线性无关 S的每个向量都可由1,.,r线性表示2. 秩S极大无关组中向量的个数3. 若秩Sr,则任何r个无关的向量都是极大无关组4. 矩阵的秩数行向量组的秩数列向量