大学物理静电场3(电势).ppt

《大学物理静电场3(电势).ppt》由会员分享，可在线阅读，更多相关《大学物理静电场3(电势).ppt（36页珍藏版）》请在第壹文秘上搜索。

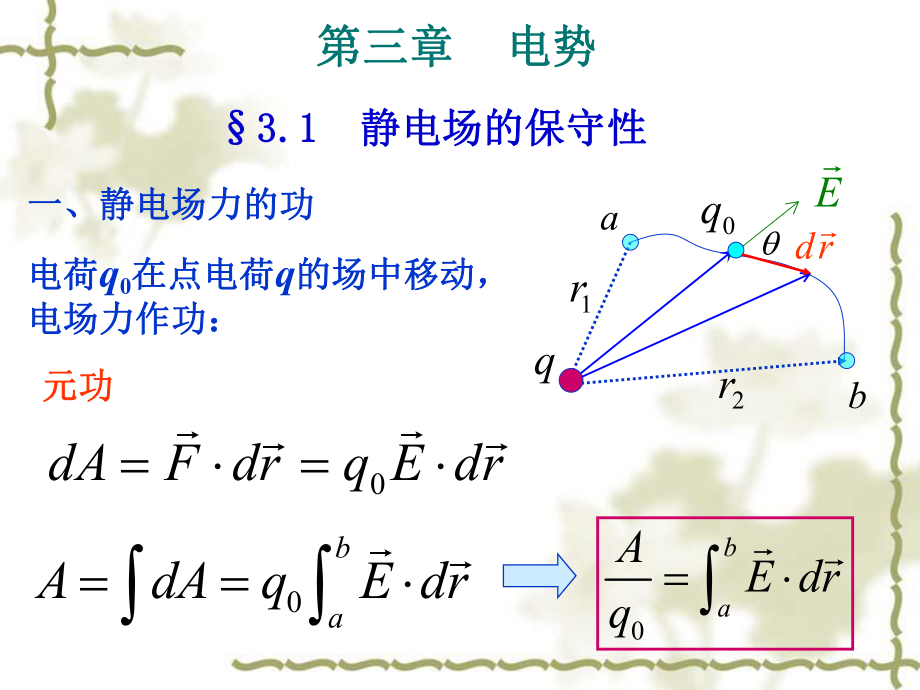
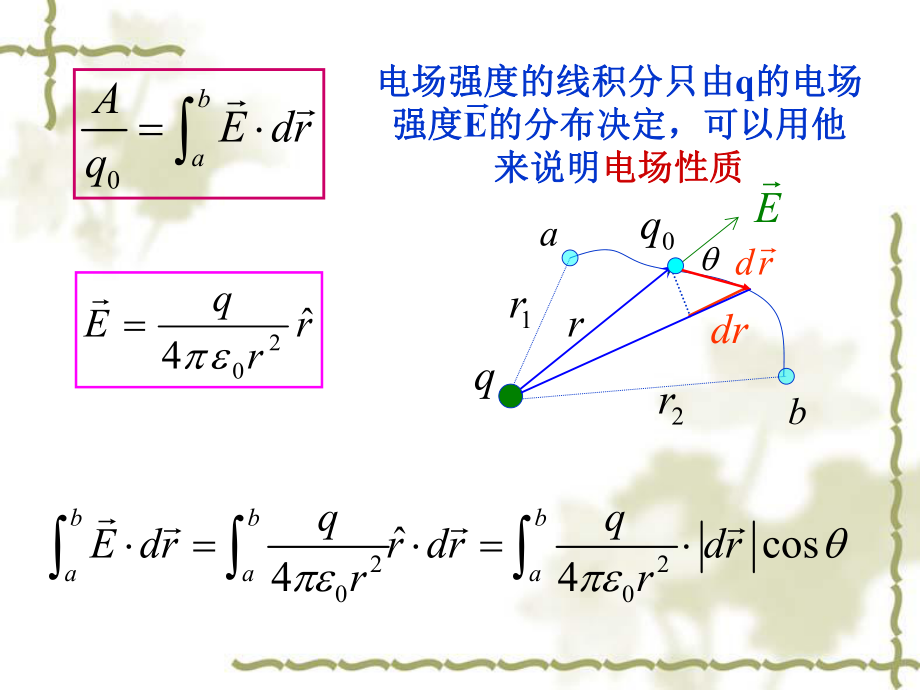
1、ab0qq1r2rEdr3.1 3.1 静电场的保守性静电场的保守性电荷电荷q0在点电荷在点电荷q的场中移动，的场中移动，电场力作功：电场力作功：一、静电场力的功一、静电场力的功元功元功0dAF drq E dr0baAdAqE dr0baAE drq第三章第三章 电势电势0baAE drq电场强度的线积分只由电场强度的线积分只由q的电场的电场强度强度E的分布决定，可以用他的分布决定，可以用他来说明来说明电场性质电场性质rrqE4202200cos44bbbaaaqqE drr drdrrrdrab0qq1r2rEdrr21200121144brarqqE drdrrrr场强的线积分与路径无关

2、场强的线积分与路径无关在静止点电荷的电场中，电场强度的线积分和积在静止点电荷的电场中，电场强度的线积分和积分路径无关（静电场力做功与路径无关）只与始分路径无关（静电场力做功与路径无关）只与始末位置有关。末位置有关。对于由多个静止点电荷组成的系统或静止的连续带对于由多个静止点电荷组成的系统或静止的连续带电体激发的场强，由场强叠加原理电体激发的场强，由场强叠加原理: :120()bbnaaAEdrEEEdrq12bbbnaaaE drEdrEdrnEEEE 21)11(410ibianiirrq积分与路径无关积分与路径无关对任何静电场，电场强度的线积分都只取决于起对任何静电场，电场强度的线积分都只

3、取决于起点和终点的位置而与积分路径无关静电场的点和终点的位置而与积分路径无关静电场的保守性保守性0LE drP1P2L2L1在静电场中，场强沿任意闭合路径的线积分等于在静电场中，场强沿任意闭合路径的线积分等于零，称为静电场的零，称为静电场的环路定理环路定理或或环流定理环流定理。静电场的保守性还可表述为：静电场的保守性还可表述为：移动单位正电荷从电场中移动单位正电荷从电场中a 点到点到b点，静电力所做点，静电力所做的功，为静电场中两点的电势差的功，为静电场中两点的电势差:3.2 电势能、电势电势能、电势电场力做功等于电场力做功等于电势能电势能的减少（或电势能的减少（或电势能增量的负值增量的负值）

4、：）：0 bababaWWAqE dr一、电势能一、电势能babababaWWUUUE drqq二、电势差：二、电势差： 只与电场有关只与电场有关描述电场的性质描述电场的性质 某点某点 (a点点) 的电势：的电势：首先设定电势首先设定电势0点（点（b点点）：）： baaUE dr电势零点的选取：原则上可任选场中一点。对于电电势零点的选取：原则上可任选场中一点。对于电荷分布在荷分布在有限区域的带电体有限区域的带电体激发的电场区域，一般选激发的电场区域，一般选无限远处时为电势零点无限远处时为电势零点, ,即即U U=0 =0 。aaUE dr在实际问题中，常在实际问题中，常常选地球的电势为常选地球

5、的电势为零电势。零电势。电势差与电势的零电势差与电势的零点选取无关。点选取无关。电势能与电势关系电势能与电势关系 Wa=qUaAab= Wa- Wb=q(Ua- Ub)沿电力线方向电势逐点沿电力线方向电势逐点降低降低(或场强总是从电势高或场强总是从电势高处指向电势低处处指向电势低处)。 电势单位：电势单位：焦耳焦耳/库仑（库仑（J / Q）、伏特（）、伏特（V）1）单个点电荷产生的电场中的电势分布。）单个点电荷产生的电场中的电势分布。 rrqE420ppUE drEqp三、电势计算三、电势计算pr负点电荷周围的场电势为负负点电荷周围的场电势为负 离电荷越远，电势越高。离电荷越远，电势越高。正点

6、电荷周围的场电势为正正点电荷周围的场电势为正 离电荷越远，电势越低。离电荷越远，电势越低。选选U=0，prrqdrrqp02044积分积分路线？路线？drrqU04 2）电势叠加原理（电势叠加原理（标量叠加标量叠加） qpUp=? pippldEldEU iirq04 rdqUp04 或对连续分布带电体或对连续分布带电体单个点电荷的场的电势单个点电荷的场的电势1q2q3qiq3r1r2rirprdqldEiP一个点电荷系的电场中一个点电荷系的电场中, ,任一点的电势等于每一个点任一点的电势等于每一个点电荷单独存在时在该点所产生电势的代数和。电荷单独存在时在该点所产生电势的代数和。电电势叠加原理

7、势叠加原理iiiarqU04电势叠加原理是以点电荷的电势公式为基础的，所以电势叠加原理是以点电荷的电势公式为基础的，所以凡是利用该原理求得的电势，电势零点都已选在了凡是利用该原理求得的电势，电势零点都已选在了无无限远处。限远处。计算电势的方法：计算电势的方法：1 1、当场强分布已知或用高斯定理易求出，、当场强分布已知或用高斯定理易求出，应用电势定义式计算电势分布。应用电势定义式计算电势分布。2 2、以点电荷电势公式为基础，应用电势、以点电荷电势公式为基础，应用电势叠加原理叠加原理( )( )0U例例1、求均匀带电球面的电场中的电势分布。、求均匀带电球面的电场中的电势分布。 设球面半径为设球面半

8、径为R，总带电量为，总带电量为Q( )rU rE dr:Rr 球面处场强不连续，电势连续球面处场强不连续，电势连续 带电球壳是个等势体。带电球壳是个等势体。drrQ)r(Ur204drrQEdrRrR204RQ04:Rr Ur0RErORPrQ04P选选U=0例例2、求无限长均匀带电直线的电场中的电势分布、求无限长均匀带电直线的电场中的电势分布rE02已知场强为：已知场强为： 方向垂直于带电直线。方向垂直于带电直线。0 ppUE dr00022rlnrln由此例看出，当电荷分布扩展到由此例看出，当电荷分布扩展到无穷远无穷远时，电势零时，电势零点点不能再选在无穷远处不能再选在无穷远处，否则，否则

9、U U。 roroppp电势零点的选取电势零点的选取积分路径的选取积分路径的选取 0 ppppUE drE drdrrp p 0020drrrr 002Crln 023321arrriiirqU04 例例3、电量分别为、电量分别为q1、q2、q3的三个点电荷位于边长为的三个点电荷位于边长为a的正三角形的三个顶点上，求该三角形中心的正三角形的三个顶点上，求该三角形中心O的电势。的电势。解：解：q1q2q3Or1r3r2)(433210oqqqaU 选选U=0? ?将带电量为将带电量为q q的点电荷从的点电荷从O O点移动到远处电场力做的功点移动到远处电场力做的功rdqdU04 21220)(4)

10、(RzqzU rqrdqdUUL0044例例4、试计算均匀带电圆环轴线上任一点、试计算均匀带电圆环轴线上任一点P的电势。的电势。设已知带电量为设已知带电量为 qZRrpdq解：解：环心处环心处RqU04选选U=0？考虑从定义出发求解？考虑从定义出发求解Z3.3 电势梯度电势梯度一、等势面一、等势面1.1.等势面等势面：将电场中电势相等的点连接起来组成的：将电场中电势相等的点连接起来组成的 曲面称为等势面。曲面称为等势面。CzyxU),(即满足即满足 的空间曲面。的空间曲面。E E等等势势面面2. 2. 等势面的性质等势面的性质 电力线与等势面垂直电力线与等势面垂直 电力线的方向指向电势降落的方

11、向电力线的方向指向电势降落的方向 若规定若规定两个相邻等势面的电势差相等，两个相邻等势面的电势差相等，则等势面较密集的地方，场强较大。则等势面较密集的地方，场强较大。babaE drUU= 0= 0点电荷的电场线与等势面点电荷的电场线与等势面+电偶极子的电场线与等势面电偶极子的电场线与等势面平行板电容器的电场线与等势面平行板电容器的电场线与等势面+2. 电势梯度电势梯度El方向方向lEabl dEUUbacosEdll dEdUUUbadldldUEElcos电场中某点场强沿某一方向的分量等于电势电场中某点场强沿某一方向的分量等于电势沿此方向的空间变化率的负值沿此方向的空间变化率的负值dldU

12、EldldU为电势沿为电势沿 方向的空间变化率方向的空间变化率ldUUUabdldUEElcosmaxdldUEl方向方向lEabdl电势梯度电势梯度电势梯度是一个电势梯度是一个矢量矢量，它的方向是该点附近，它的方向是该点附近电势电势升高最快升高最快的方向的方向电场中任一点的场强等于该点电势梯度的电场中任一点的场强等于该点电势梯度的负值负值，即，即场强指向场强指向电势降低电势降低的方向的方向maxdldUEyUEy xUEx 在直角坐标系中：在直角坐标系中：zUEz kzjyixgrad 梯度算符梯度算符UgradUE电势是空间坐标的函数电势是空间坐标的函数zyxU,)(kzUjyUixUE)

13、(kzUjyUixUUE 电场强度与电势的微分关系电场强度与电势的微分关系该公式说明，电场中某点的场强决定于电势在该点该公式说明，电场中某点的场强决定于电势在该点的的空间变化率空间变化率，而与该点，而与该点电势值本身电势值本身无直接关系无直接关系给出求电场的又一方法：由给出求电场的又一方法：由电荷分布电荷分布 U E2122004 4/)xR(qrqU例例. 求均匀带电圆环轴线上的场强分布求均匀带电圆环轴线上的场强分布232204)xR(qxidxdUUEi)xR(qx232204oxRqxrdxdUxEE P计算场强的方法计算场强的方法1 1、以点电荷场强公式为基础，应用场强叠加原、以点电荷

14、场强公式为基础，应用场强叠加原理求场强分布。原则上这种方法可计算任何带电理求场强分布。原则上这种方法可计算任何带电体激发的电场分布，主要体激发的电场分布，主要困难困难是是积分运算积分运算。2 2、当电荷分布具有对称性时可用、当电荷分布具有对称性时可用高斯定理高斯定理求场求场强分布。强分布。3 3、若电势分布已知，则可利用、若电势分布已知，则可利用 求出场强分布。求出场强分布。UE 1.两个物理量两个物理量2.两个基本性质方程两个基本性质方程3.两个计算思路两个计算思路真空中静电场小结（真空中静电场小结（两两歌两两歌）UE00LiiSlEqSEdd QQUUEEdd)0()(0PiiSlEUqS

15、Edd叠加叠加与与高斯高斯注重典型场注重典型场 注重叠加原理注重叠加原理 rQUrrQE02044rE0202E无限长柱面？无限长柱面？第第3章结束章结束rQUrrQERrRQUERr020044404.强调两句话强调两句话两个同心均匀带电球面的电场和电势两个同心均匀带电球面的电场和电势的叠加的叠加1 1、已知电场中某点的场强，能否计算出该、已知电场中某点的场强，能否计算出该点的电势？点的电势？2 2、在电势不变的空间，场强是否不变、在电势不变的空间，场强是否不变? ?3 3、电势为零处，场强是否一定为零？、电势为零处，场强是否一定为零？4 4、场强为零处，电势是否一定为零？、场强为零处，电势

16、是否一定为零？思考以下问题？思考以下问题（要已知场强分布）（要已知场强分布）是，是，0gradUE电偶极子的中垂线，电势为零，但电场不为零电偶极子的中垂线，电势为零，但电场不为零均匀带电球面的内部，场强为零，电势不为零均匀带电球面的内部，场强为零，电势不为零下面说法正确的是下面说法正确的是 D (A)等势面上各点场强的大小一定相等；等势面上各点场强的大小一定相等；(B)在电势高处，电势能也一定高；在电势高处，电势能也一定高； (C)场强大处，电势一定高；场强大处，电势一定高；(D)场强的方向总是从电势高处指向低处场强的方向总是从电势高处指向低处. .例. .一带电细线弯成半径为一带电细线弯成半径为 R 的半圆形，电荷线密的半圆形，电荷线密度为度为 =0sin，式中，式中 为半径为为半径为 R 与与 x 轴所成的轴所成的夹角，夹角，0 为一常数，如图所示，试求环心为一常数，如图所示，试求环心 o 处的电处的电场强度。场强度。0 xyR解：在解：在 处取电荷元，处取电荷元，其电量为其电量为dldq它在它在o点处产生的场强为点处产生的场强为204RdqdE0 xydEydExdEdqRd00