华中农业大学微积分方红第七章第二节.ppt

《华中农业大学微积分方红第七章第二节.ppt》由会员分享，可在线阅读，更多相关《华中农业大学微积分方红第七章第二节.ppt（22页珍藏版）》请在第壹文秘上搜索。

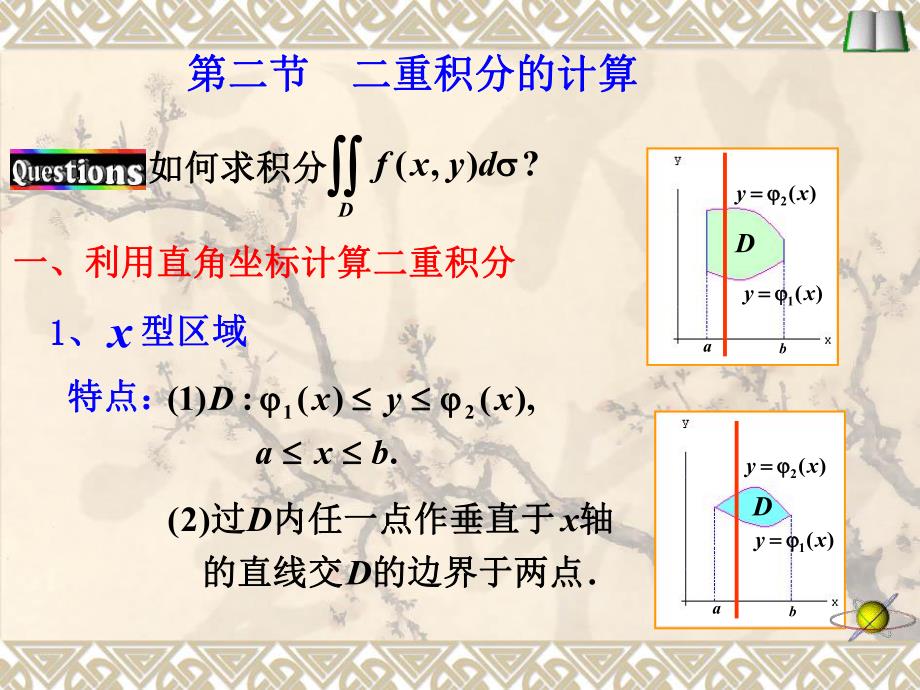
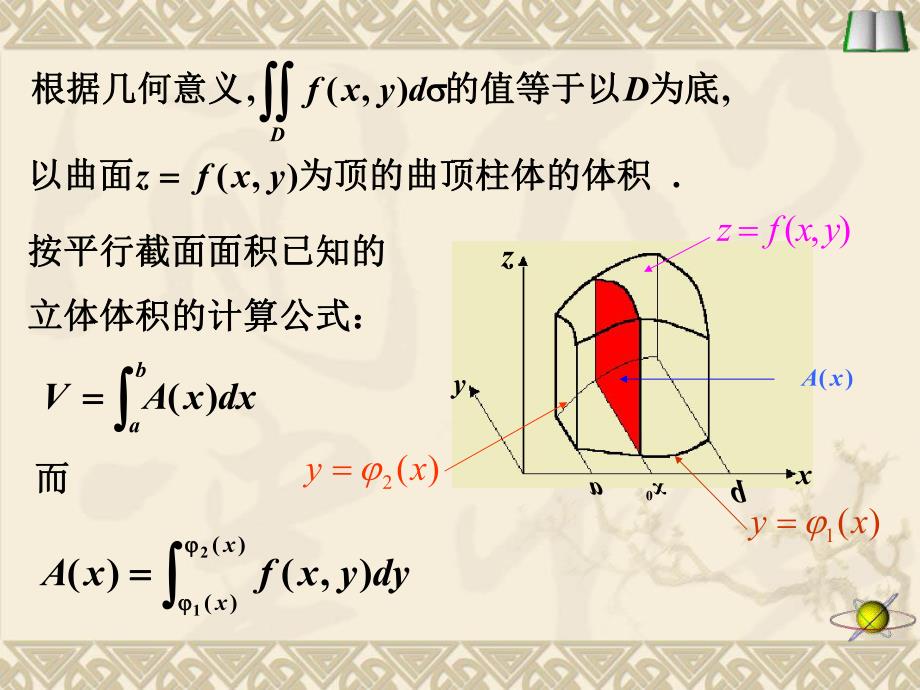
1、第二节第二节 二重积分的计算二重积分的计算 一、利用直角坐标计算二重积分一、利用直角坐标计算二重积分 x1 1、型区域型区域 )(2xy abD)(1xy Dba)(2xy )(1xy 特点：特点：.),()(:)1(21bxaxyxD .)2(的边界于两点的边界于两点的直线交的直线交轴轴内任一点作垂直于内任一点作垂直于过过DxD如何求积分如何求积分?),(Ddyxf.),(,),(,为顶的曲顶柱体的体积为顶的曲顶柱体的体积以曲面以曲面为底为底的值等于以的值等于以根据几何意义根据几何意义yxfzDdyxfD a0 xbzyx)(xA),(yxfz)(1xy)(2xy按平行截面面积已知的按平行截

2、面面积已知的 立体体积的计算公式：立体体积的计算公式：badxxAV)(而而 )()(21),()(xxdyyxfxAdxdyyxfdyxfDbaxx )()(21),(),(*),()()(21 xxbadyyxfdx由此得二重积分计算公式：由此得二重积分计算公式：即化二重积分为二次积分。即化二重积分为二次积分。(*)式表示先对式表示先对 )()(21 ),(xxdyyxf积分，积出来后得积分，积出来后得 x的函数，将其作为被积函数放到第的函数，将其作为被积函数放到第 到一个关于到一个关于 一个积分里再积；而不是两个积分的简单乘积。一个积分里再积；而不是两个积分的简单乘积。y2 2、型区域型

3、区域 )(2yx )(1yx Dcdcd)(2yx )(1yx D特点：特点：;),()(:)1(21dycyxyD .)2(的边界于两点的边界于两点轴的直线交轴的直线交内任一点作垂直于内任一点作垂直于过过DyD类似于前面的方法，可得到二重积分的计算公式：类似于前面的方法，可得到二重积分的计算公式：dydxyxfdyxfDdcyy )()(21),(),()()(21),(yydcdxyxfdy3D2D1D如果积分区域如右图，则需分割为：如果积分区域如右图，则需分割为：321DDDD 由积分的可加性，得由积分的可加性，得 .321 DDDD例例1 1、.,2,1,所围所围由直线由直线其中其中计

4、算计算xyxyDxydxdyD 例例2 2、.,)(222所围所围由抛物线由抛物线其中其中计算计算yxxyDdxdyyxD 例例3 3、.1,1,122所围所围由由其中其中计算计算 yxxyDdxdyyxyD（1 1）画出积分区域）画出积分区域D。（2 2）选择恰当的积分区域类型。）选择恰当的积分区域类型。（3 3）定出积分限，通过二次积分求出二重积分。）定出积分限，通过二次积分求出二重积分。投影穿刺法投影穿刺法计算二重积分的一般步骤：计算二重积分的一般步骤：例例4 4、.)1,0(),1,1(),0,0(,22为顶点的三角形区域为顶点的三角形区域是以是以其中其中计算计算DdxdyexDy 例

5、例5 5、.,:,)()()()(:dycbxaDdyygdxxfdxdyygxfdcDba 其中其中证明证明例例6 6、交换下列逐次积分的次序。、交换下列逐次积分的次序。.),(),()3(;),()2(;),()1(102120201011101022 xxxyyxdyyxfdxdyyxfdxdxyxfdydyyxfdx例例7 7、214112121.dxedydxedyIyyxyyxy计算积分计算积分例例8 8、.10,10:,2 yxDdxdyxyD其中其中计算计算例例9 9、用二重积分求下列曲（平）面所围成立体的体积。、用二重积分求下列曲（平）面所围成立体的体积。.0,0,1,)3(

6、;0,1,0,0),()2(;,)1(222222 yxyxxyzyxzzxyxyxyxxzRzxRyx求体积关键：画出投影区域求体积关键：画出投影区域D，想象出曲顶。，想象出曲顶。例例1010、求下列积分。、求下列积分。others ,020,10 ,1),(),(1yxyxfdxdyyxfxy）（others ,020,20 ,),(),(22xyxxyyxfdxdyyxfzyx）（练练 习习 题题 .)()(,)(,1,0)(.3.1:.2),()4(),(),()2(),()3(),(),()1(:.110101101440442182820221020212032222 xyyyyx

7、xxaaxxaxxxxdyyfxfdxAdxxfCxfdxxdydxyxfdydyyxfdxdyyxfdxdyyxfdxdyyxfdxdyyxfdx求求并设并设设设计算二重积分计算二重积分更换下列积分次序更换下列积分次序作业作业习题习题7-27-2（1 1）：）：1 1（奇数题）、（奇数题）、5 5 （奇数题）（奇数题）二、利用极坐标计算二重积分二、利用极坐标计算二重积分 AoDdrr r d 如右图，极坐标下面积元素：如右图，极坐标下面积元素：rdrddxdyd由此得二重积分在极坐标下由此得二重积分在极坐标下 的表达式为：的表达式为：DDDrdrdrrfdxdyyxfdyxf)sin,cos

8、(),(),(d如何定限化二重积分为二次积分？如何定限化二重积分为二次积分？ADo情形情形1 1：特征如下图特征如下图 ,).()(21 rrr积分公式如下：积分公式如下：rdrrrfdrdrdrrfDrr)sin,cos()sin,cos()()(21 )(1 rr)(2 rrAoD)(2 rr)(1 rr情形情形2 2：特征如右图特征如右图 ,).(0 rrAoD)(rrrdrrrfdrdrdrrfDr)sin,cos()sin,cos()(0 积分公式如下：积分公式如下：情形情形3 3：特征如右图特征如右图 ).(0 rrDoA)(rr,20 积分公式如下：积分公式如下：rdrrrfdr

9、drdrrfDr)sin,cos()sin,cos(20)(0 （1 1）直角坐标下：）直角坐标下：（2 2）极坐标下：）极坐标下：.Drdrd;Ddxdy例例1 1、.10,11:,),(2 xxyxDdxdyyxfD其中其中的极坐标形式的极坐标形式写出积分写出积分例例2 2、.2:)2(.0,0,:,)1(0222)(222 dxeyxayxDdxdyexDyx证明证明计算积分计算积分面积公式：面积公式：例例3 3、.03,034,2,)(222222的平面闭区域的平面闭区域所围成所围成及直线及直线为圆为圆其中其中计算积分计算积分 xyyxyyxyyxDdxdyyxD例例4 4、.2222

10、22所围体积所围体积与圆柱面与圆柱面求球面求球面axyxazyx 例例5 5、.)(2)(222222222所围成的图形的面积所围成的图形的面积和和求曲线求曲线ayxyxayx .,22方法积分方法积分时通常可以考虑极坐标时通常可以考虑极坐标式中含有式中含有表达表达当被积函数和积分区域当被积函数和积分区域由上面例子可以看到由上面例子可以看到yx aaaaadxxfdxxfxfdxxfxf0.)(2)(,)(;0)(,)(:)1(为偶函数时为偶函数时为奇函数时为奇函数时定积分中定积分中 DDyxfyxfdxdyyxfyxfyxfdxdyyxfxDyyxf1),(),(),(2),(),(0),(

11、,),(:)2(则则轴对称轴对称关于关于积分区域积分区域的奇偶函数的奇偶函数为为二重积分中二重积分中.1在上半平面部分在上半平面部分为为DD关于积分中对称性的应用：关于积分中对称性的应用：DDyxfyxfdxdyyxfyxfyxfdxdyyxfyDxyxf2),(),(),(2),(),(0),(,),(则则轴对称轴对称关于关于积分区域积分区域的奇偶函数的奇偶函数为为.2在右半平面部分在右半平面部分为为DD DDyxfyxfdxdyyxfyxfyxfdxdyyxfDyxyxf1),(),(),(2),(),(0),(,),(则则关于原点对称关于原点对称积分区域积分区域的奇偶函数的奇偶函数同时为

12、同时为.1在上半平面部分在上半平面部分为为DD DDdxdyxyfdxdyyxfxyD.),(),(,则则对称对称关于直线关于直线若若例例6 6、2121212132223221212.4.4.4.)(,)(,)(,20,10:;22,11:21IIDIICIIBIIAdxdyyxIdxdyyxIyxDyxDDD 则有则有又又设区域设区域C例例8 8、.41:,)sin(222222 yxDdxdyyxyxD计算积分计算积分例例7 7、0.)sincos(4.2.sincos2.)()sincos(,)1,1()1,1(),1,1(1111DdxdyyxxyCxydxdyBydxdyxAdxd

13、yyxxyDDxoyDDDDD 等于等于则则在第一象限的部分在第一象限的部分是是的三角形区域的三角形区域为顶点为顶点和和面上以面上以是是设设A三、利用换元法计算二重积分三、利用换元法计算二重积分 定理：定理：.),(),(),(),(,:)3(;0),(),(),()2();(),(),()1(:,),(),(:,),()1(dudvvuJvuyvuxfdxdyyxfDDTvuyxvuJDCvuyvuxDxoyDuovvuyyvuxxTDxoyyxfDD 则有则有是一对一的是一对一的变换是变换是且满足且满足面上的面上的变为变为面上的闭区域面上的闭区域将将变换变换上连续上连续面上的闭区域面上的闭

14、区域在在设设例例1 1、.2,所围成的闭区域所围成的闭区域和直线和直线轴轴轴轴为由为由其中其中计算积分计算积分 yxyxDdxdyeDxyxy例例2 2、.1:,122222222 byaxDdxdybyaxD计算积分计算积分Dxyo2 yxD uvovu vu 2 v练练 习习 题题 作业作业习题习题7-27-2（2 2）：）：2 2（1 1）（）（3 3）、）、3 3 .20,42:,)(.4.2 ,0,0,.3.4:,sin.2.),()2(;)sin,cos()1(.12222222222222222220cos02 xxyxxDdxdyyxRxyxRyxyxDdxdyyxyxDdxdyyxdyyxfdxrdrrrfdDDDaaaax其中其中计算计算围成围成和和由由其中其中计算计算其中其中计算计算标积分互化标积分互化将下列直角坐标与极坐将下列直角坐标与极坐第一象限区域。第一象限区域。