钢结构设计原理6拉弯和压弯构件.ppt

《钢结构设计原理6拉弯和压弯构件.ppt》由会员分享，可在线阅读，更多相关《钢结构设计原理6拉弯和压弯构件.ppt（54页珍藏版）》请在第壹文秘上搜索。

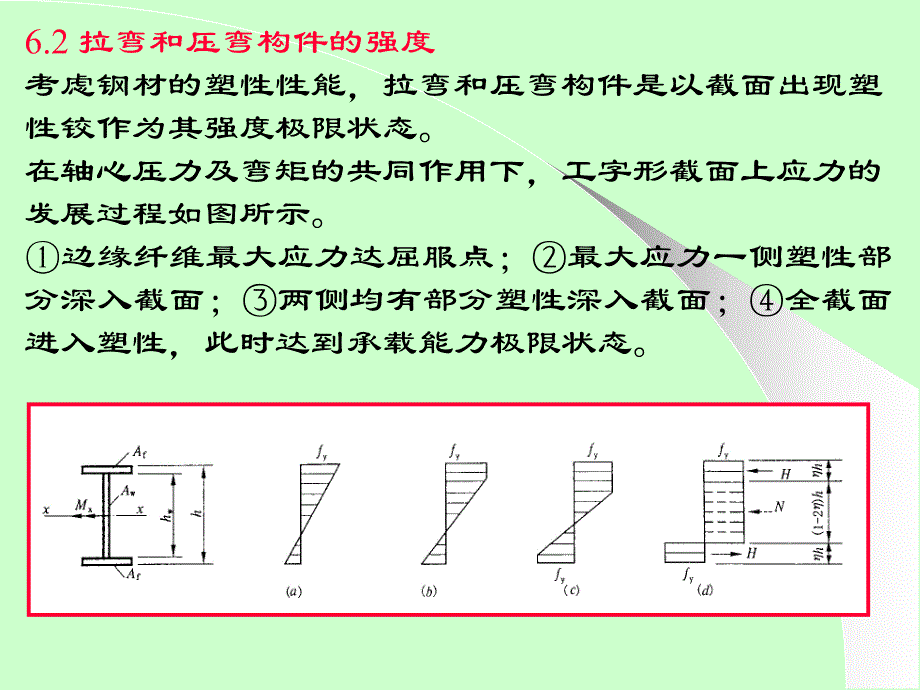
1、第六章 拉弯和压弯构件6.1 拉弯和压弯构件的特点 拉弯或压弯构件：同时承受轴向力和弯矩的构件。压弯和拉弯构件的应用十分广泛，例如有节间荷载作用的桁架上下弦杆，受风荷载作用的墙架柱以及天窗架的侧立柱，工业建筑中的厂房框架柱，不仅要承受上部结构传下来的轴向压力，同时还受有弯矩和剪力。设计拉弯和压弯构件时，应同时满足承载能力极限状态和正常使用极限状态的要求。拉弯构件需要计算其强度和刚度(限制长细比)；压弯构件则需要计算强度、整体稳定(弯矩作用平面内稳定和弯矩作用平面外稳定)、局部稳定和刚度(限制长细比)。6.2 拉弯和压弯构件的强度考虑钢材的塑性性能，拉弯和压弯构件是以截面出现塑性铰作为其强度极限

2、状态。在轴心压力及弯矩的共同作用下，工字形截面上应力的发展过程如图所示。边缘纤维最大应力达屈服点；最大应力一侧塑性部分深入截面；两侧均有部分塑性深入截面；全截面进入塑性，此时达到承载能力极限状态。whh wfAAwAA)12(根据内外力平衡条件，由一对水平力H所组成的力偶与外力矩M平衡，合力N应与外轴力平衡，为了简化，取内力的计算分为两种情况：(1)中和轴在腹板范围内ywfAN ywywfAfhtN)21()21()()1(2ywywyfxhfAhfAhfAMywypfAAfN)12(ywywwypxpxhfAfhAhAfWM)25.0()25.0(114)12(222pxxpMMNN(2)中

3、和轴在翼缘范围内 ywfAN 1)12(214ppxxNNMM图中实线为工字形截面构件当弯矩绕强轴作用时的相关曲线。曲线是外凸的，但腹板面积较小时外凸不多。为了便于计算，同时考虑分析中没有考虑附加挠度的不利影响，规范采用了直线式相关公式，即用斜直线代替曲线。1ppxxNNMM承受双向弯矩的拉弯或压弯构件，采用了与上式相衔接的线性公式fWMWMANnyyynxxxn当压弯构件受压翼缘的自由外伸宽度与其厚度之比 但不超过 时，应取 。需要计算疲劳的拉弯和压弯构件，宜取 yf/23515yftb/23513/0.1yx0.1xfWMANnxxxnynpfAN令 ，引入抗力分项系数，得到拉弯和压弯构件

4、的强度计算式 ynxxpxfWM6.3 实腹式压弯构件的整体稳定压弯构件的截面尺寸通常由稳定承载力确定。双轴对称截面一般将弯矩绕强轴作用，单轴对称截面则将弯矩作用在对称轴平面内。构件可能在弯矩作用平面内弯曲失稳，也可能在弯矩作用平面外弯扭失稳。所以，压弯构件要分别计算弯矩作用平面内和弯矩作用平面外的稳定性。6.3.1 弯矩作用平面内的稳定计算 目前确定压弯构件弯矩作用平面内极限承载力的方法很多，可分为两大类，一类是边缘屈服准则的计算方法，一类是精度较高的数值计算方法。1.边缘屈服准则横向荷载产生的跨中挠度为vm 。当荷载对称时，假定挠曲线为正弦曲线。轴心力作用后，挠度增加，在弹性范围，跨中挠度

5、增加为l(1a)称为挠度放大系数。跨中总弯矩为 等效弯矩系数。m1111111maxMMNvMMNvMvNMMmmmm1maxmvv根据各种荷载和支承情况产生的跨中弯矩M和跨中挠度可以计算出相应的等效弯矩系数。弹性压弯构件，可用截面边缘屈服作为稳定计算准则。假定各种缺陷的等效初弯曲呈跨中挠度为 的正弦曲线。任意横向荷载或端弯矩作用下的计算弯矩为M，则跨中总弯矩应为构件中点截面边缘纤维达到屈服时令M0，即有初始缺陷的轴心压杆边缘屈服时表达式 EmNNNvMM/10maxyEmfWNNNvMAN/10yEfWNNvNAN000010v 经整理得 边缘屈服准则导出的相关公式。规范将上式作为格构式压弯

6、构件绕虚轴平面内稳定计算的相关公式，引入抗力分项系数AWNAfvEy1)11(0yEfNNWMAN1myfAN0fNNWMANExxxxx11m2.最大强度准则 边缘屈服准则当截面最大受压纤维屈服时构件失去承载能力，适用于格构式构件。实腹式当受压最大边缘刚屈服时尚有较大的强度储备，即容许截面塑性深入。因此宜采用最大强度准则，以具有初始缺陷的构件为计算模型，求解极限承载力。采用数值计算方法，考虑l1000的初弯曲和实测的残余应力，算出了近200条压弯构件极限承载力曲线。不同的截面形式或截面形式相同但尺寸不同、残余应力的分布不同以及失稳方向的不同等，其曲线都将有很大的差异。200条曲线很难用一统一

7、公式来表达。分析证明采用相关公式的形式可较好地解决。影响极限承载力的因素很多，要得到精确的、符合各种不同情况的理论公式是不可能的。因此，只能根据理论分析的结果，经过数值运算，得出比较符合实际又能满足工程精度要求的实用相关公式。3 规范计算公式将用数值方法得到的压弯构件的极限承载力与用边缘纤维屈服准则导出的相关公式中的轴心压力进行比较，对于短粗的实腹杆，偏于安全；对于细长的实腹杆，偏于不安全。因此借用了边缘纤维屈服时计算公式的形式，但计算弯曲应力时考虑了截面的塑性发展和二阶弯矩，初弯曲和残余应力的影响综合为一个等效偏心距，弯矩为非均匀分布时，用等效弯矩代替，考虑部分塑性深入截面，并引入抗力分项系

8、数，得到实腹式压弯构件弯矩作用平面内的稳定计算式fNNWMANExxxxmxx18.01fNNWMANExxxxx11m 等效弯矩系数，按下列情况取值：(1)框架柱和两端支承的构件：无横向荷载作用时：，M1和M2 为端弯矩，使构件产生同向曲率(无反弯点)时取同号，使构件产生反向曲率(有反弯点时)取异号 有端弯矩和横向荷载同时作用时：使构件产生同向曲率时，；使构件产生反向曲率时，；无端弯矩但有横向荷载作用时：。(2)悬臂构件和未考虑二阶效应的无支撑纯框架和弱支撑框架，。21MM 12/35.065.0MMmx0.1mx0.1mxmx0.1mx85.0mx对于T形截面等单轴对称压弯构件，当弯矩作用

9、于对称轴平面且使较大翼缘受压时，构件失稳时出现的塑性区除存在前述受压区屈服和受压、受拉区同时屈服两种情况外，还可能在受拉区首先出现屈服而导致构件失去承载力，还应按下式计算 式中 受拉侧最外纤维的毛截面模量。上式第二项分母中的系数1.25也是经过与理论计算结果比较后引进的修正系数。fNNWMANExxxxmx225.11xW26.3.2 弯矩作用平面外的稳定计算 开口薄壁截面压弯构件的抗扭刚度及弯矩作用平面外的抗弯刚度通常较小，当构件在弯矩作用平面外没有足够的支撑以阻止其产生侧向位移和扭转时，构件可能因弯扭屈曲而破坏。构件在发生弯扭失稳时，其临界条件为 可以画出相关曲线如图所示。0112crxx

10、zEyEyEyMMNNNNNN如偏安全地取 1.0，则上式成为 EyzNN/221EycrxxNNMM1crxxEyMMNN 并引入非均匀弯矩作用时的等效弯矩系数、箱形截面的调整系数以及抗力分项系数后，得到压弯构件在弯矩作用平面外稳定计算的相关公式为 所计算构件段范围内(构件侧向支承点间)的最大弯矩；等效弯矩系数，应根据所计算构件段的荷载和内力情况确定，取值方法与弯矩作用平面内的等效弯矩系数相同。xybcrxWfM1AfNyyEyfWMANxbxtxy1xMtx 调整系数，箱形截面0.7，其他截面1.0；弯矩作用平面外的轴心受压构件稳定系数；均匀弯曲梁的整体稳定系数，可采用近似计算公式。yb6

11、.3.3双向弯曲实腹式压弯构件的整体稳定弯矩作用在两个主轴平面内为双向弯曲压弯构件，工程中较为少见。规范规定了双轴对称截面的计算方法。双轴对称的工字形截面(含H型钢)和箱形截面压弯构件的整体稳定计算fWMNNWMANxbyytyExxxxmxx18.01fWMNNWMANxbxxtxEyyyymyy8.016.4 实腹式压弯构件的局部稳定 为保证压弯构件中板件的局部稳定，限制翼缘和腹板的宽厚比及高厚比。6.4.1 受压 翼缘的宽厚比 压弯构件受压翼缘应力情况与梁受压翼缘基本相同，因此自由外伸宽度与厚度之比以及箱形截面翼缘在腹板之间的宽厚比均与梁受压翼缘的宽厚比限值相同。6.4.2 腹板的高厚比

12、 1.工字形截面 平均剪应力和不均匀正应力共同作用下，临界条件 1221211211501150crcrcrmaxminmax0对压弯构件，腹板中剪应力的影响不大，平均剪应力可取腹板弯曲应力的0.3倍，腹板弹性屈曲临界应力为式中，ke为弹性屈曲系数，其值与应力梯度有关。腹板的弹塑性临界应力为式中，kp为塑性屈曲系数，其值与构件的长细比和应力梯度有关。取临界应力为235N/mm2，可得到腹板高厚比与应力梯度之间的关系，此关系可近似地用直线式表示 2022)1(12htEkwecr2022)1(12htEkwpcr6.1005016/00wth0.26.10148/00wth6.100ywfth2

13、35)255.016(000.26.10ywfth235)2.265.048(00长细比较小的压弯构件，整体失稳时截面的塑性深度实际上已超过了0.25h0，长细比较大的压弯构件，截面塑性深度则不到0.25 h0，甚至腹板受压最大的边缘还没有屈服。因此，h0/tw之值宜随长细比的增大而适当放大。工字形截面压弯构件腹板高厚比限值 ywfth235180ywfth2351500.100.102.T形截面 (1)弯矩使腹板自由边受压当 (弯矩较小)时，T形截面腹板中压应力分布不均的有利影响不大，宽厚比限值采用与翼缘板相同；当 (弯矩较大)时，有利影响较大，故提高200.100.10(2)弯矩使腹板自由

14、边受拉热轧剖分T形钢焊接T形钢ywfth235)2.015(0ywfth235)17.013(06.100ywfth235)255.016(8.0000.26.10ywfth235)2.265.048(8.0003.箱形截面 两腹板受力可能不一致，翼缘对腹板的约束因常为单侧角焊缝也不如工字形截面，因而箱形截面的宽厚比限值取为工字形截面腹板的0.8倍。yf23540不小于yftD2351004.圆管截面 一般圆管截面构件的弯矩不大，故其直径与厚度之比的限值与轴心受压构件的规定相同。6.5 压弯构件的计算长度端部约束条件比较简单的单根压弯构件，利用计算长度系数可直接得到计算长度。对于框架柱，平面内

15、的计算长度需通过框架整体稳定分析得到，平面外的计算长度则需根据支撑点的布置情况确定。6.5.1 单层等截面框架柱在框架平面内的计算长度进行框架的整体稳定分析时，一般取平面框架作为计算模型，不考虑空间作用。框架分为无支撑框架和有支撑框架，其中有支撑框架根据抗侧移刚度的大小分为强支撑框架和弱支撑框架。当支撑结构(支撑桁架、剪力墙、电梯井等)的侧移刚度(产生单位侧倾角的水平力)Sb满足下式要求时，为强支撑框架 Sb3(1.2NbiN0i)当支撑结构的侧移刚度Sb不满足上式的要求时，为弱支撑框架。强支撑框架的失稳形式一般为无侧移的，弱支撑框架的失稳形式为有侧移的。有侧移失稳的框架其临界力比无侧移失稳的

16、框架低得多。因此，除非有阻止框架侧移的支撑体系(包括支撑架、剪力墙等)，框架的承载能力一般以有侧移失稳时的临界力确定。1.无支撑框架 (1)一阶弹性分析方法框架柱的上端与横梁刚性连接。横梁对柱的约束作用取决于横梁的线刚度与柱的线刚度的比值 对于单层多跨框架，值为与柱相邻的两根横梁的线刚度之和与柱线刚度之比 HIlIK/11HIlIlIK/22111框架柱在框架平面内的计算长度可用下式表达 式中 H柱的几何长度；计算长度系数，与框架柱柱脚与基础的连接形式及 值有关。HH01K有侧移的无支撑框架失稳时，框架柱的 值都大于1.0。柱脚刚接的有侧移无支撑框架柱，值约在1.02.0之间。柱脚铰接的有侧移无支撑纯框架柱，值总是大于2.0。（2）二级弹性分析方法当采用二阶弹性分析方法计算内力且在每层柱顶附加考虑假想水平力Hni时，=1.0。Qi第i楼层的总重力荷载设计值；ns框架总层数；y钢材强度影响系数，其值为：对Q235钢1.0；Q345钢1.1；Q390钢1.2；Q420钢1.25。siyninQH12.02502.有支撑框架（1）强支撑框架无侧移的强支撑框架框架，值小于1，查表得。（2）弱支