第8章频谱的非线性搬移.ppt

《第8章频谱的非线性搬移.ppt》由会员分享，可在线阅读，更多相关《第8章频谱的非线性搬移.ppt（53页珍藏版）》请在第壹文秘上搜索。

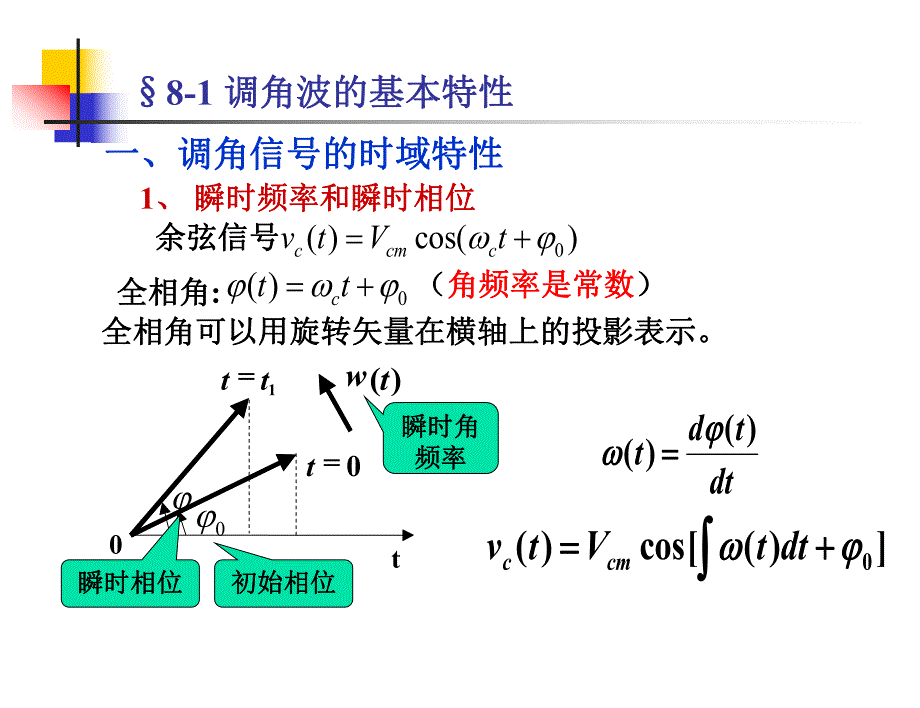
1、 第第 8 章章 角角 度度 调调 制制与与解解 调调 电电 路路 全相角可以用旋转矢量在横轴上的投影表示。全相角可以用旋转矢量在横轴上的投影表示。一、调角信号的时域特性一、调角信号的时域特性8-1 调角波的基本特性调角波的基本特性 1、瞬时频率和瞬时相位瞬时频率和瞬时相位dttdt)()()(cos)(0 dttVtvcmc0t0=t1tt=)(tw0)cos()(0tVtvccmc余弦信号余弦信号0)(ttc全相角全相角:（角频率是常数角频率是常数）初始相位初始相位瞬时角瞬时角频率频率瞬时相位瞬时相位2、调频信号、调频信号 在频率调制时，使余弦信号的在频率调制时，使余弦信号的瞬时角频率与瞬

2、时角频率与调制信号成线性关系变化调制信号成线性关系变化，而初始相位不变。，而初始相位不变。tfccmFMdvktVtv 0 0)(cos)(调频信号调频信号c为中心角频率（即载波角频率）为中心角频率（即载波角频率）kf为比例常数，单位是为比例常数，单位是rad/sv)()(tvktfcf瞬时角频率瞬时角频率为：为：tffdt 0 0)()(瞬时相位瞬时相位为：为：3、调相信号、调相信号 相位调制时，保持余弦信号的中心角频率相位调制时，保持余弦信号的中心角频率 不变，不变，而使其而使其瞬时相位与调制信号成线性关系变化瞬时相位与调制信号成线性关系变化。c 0)(cos)(tvktVtVpccmPM

3、调相信号调相信号0)()(tvkttpcp瞬时相位瞬时相位为：为：kp为比例常数，单位是为比例常数，单位是rad/vdttdtpp)()(瞬时角频率瞬时角频率为：为：4、单音调角波的数学表示式、频移和相移、单音调角波的数学表示式、频移和相移假定未调载波表示为：假定未调载波表示为：)(cos)cos()(tVtVtvcmccmc 调制信号为：调制信号为：tVtvm cos)(调频波的瞬时角频率调频波的瞬时角频率为：为：tVktvktmfcfcf cos)()(频移的幅度，称为频移的幅度，称为最大频偏或简称频偏最大频偏或简称频偏:mfmVk 瞬时角频偏瞬时角频偏：ttVktmmf coscos)(

4、调频波的瞬时相位调频波的瞬时相位0 0 0 0 0sincos)()(tVktdVkdtmfctmfctff附加相移部分附加相移部分：tMtVktfmff sinsin)(调频波的最大附加相移为调频波的最大附加相移为调频指数调频指数Mf：FfVktMmmmfff max)(Mf可以小于可以小于1，也可大于，也可大于1 正比于正比于 ，反比于，反比于 。）（即（即mmV fM调频波的数学表示式调频波的数学表示式以单频余弦波作调制信号的调频波，其主要性质有：以单频余弦波作调制信号的调频波，其主要性质有：频偏决定于调制信号的振幅，瞬时频率的变化规律频偏决定于调制信号的振幅，瞬时频率的变化规律决定于调

5、制信号的变化规律。决定于调制信号的变化规律。调频波的幅度为常数。调频波的幅度为常数。调频波的调制指数可大于调频波的调制指数可大于1，而且通常应用于大于，而且通常应用于大于1的的情况。调制指数与频偏成正比，与调制频率成反比。情况。调制指数与频偏成正比，与调制频率成反比。sincossincos00 tMtVtVktVfccmmfccm)(cos)(tVtvfcmFM 0sin)(tVkttmfcf调相波的数学表示式调相波的数学表示式 调相波的瞬时相位为：调相波的瞬时相位为：00cos)()(tVkttvkttmpcfpcp 调相波的最大附加相移调相波的最大附加相移Mp 称为调相指数称为调相指数m

6、PfPPPVktvktM maxmax)()(调相波的瞬时角频率为调相波的瞬时角频率为：)()()(tdttdtPcPP 调相波：调相波：coscoscoscos)(cos)(00 tMtVtVktVtVtvPccmmPccmpcmPMmppVkM 瞬时角频偏为瞬时角频偏为：tMdttVdktpmpP sincos)(单音调角信号参数比较单音调角信号参数比较表达式表达式最大附加相移最大附加相移（调制指数）（调制指数）最大频偏最大频偏附加相位附加相位瞬时相位瞬时相位瞬时角频偏瞬时角频偏瞬时角频率瞬时角频率相位调制相位调制频率调制频率调制tVktmfcf cos)(mfmVk tVktmff co

7、s)(tVkttmfcf sin)(/mffmVkM tVktmff sin)/()()sincos()(tMtVtvfccmFM mppVkM tVkttmpcp cos)(tMtpP sin)(tVktmpcP sin)(tVktmpp cos)(mpmVk)coscos()(tMtVtvPccmPM 单音调制波形单音调制波形t)(tvFM)(tvmVt0)(tfmt0)(tffMt0t)(tvPM)(tvmVt0t)(tppM0)(tpmt0二、调角信号的频域特性二、调角信号的频域特性调制信号为：调制信号为：tVtvm cos)(调频波的表示式为：调频波的表示式为：sincos)(tMt

8、tvfcFM 下面分析单频余弦信号调制下，调频波的频谱。下面分析单频余弦信号调制下，调频波的频谱。)sinsin(sin)sincos(cos)(tMttMttvfcfcFM 式中，出现了式中，出现了 两个特殊函数。两个特殊函数。)sinsin()sincos(tMtMff 和和tnMJttMJttMJttMJtMJtvcfnnccfccfccfcfFM)cos()()3cos()3)cos()2cos()2)cos()cos()cos(cos)()(3210 的的第第一一类类贝贝塞塞尔尔函函数数是是宗宗数数为为其其中中，ffnMMJ)(利用三角函数公式，展开可得：利用三角函数公式，展开可得：

9、)sinsin(sin)sincos(cos)(tMttMttvfcfcFM 1、第一类贝塞尔函数、第一类贝塞尔函数 的性质的性质：)(fnMJfM)(fnMJ0n1234 nfnMJ1)(32、10)(4 ffnfMnMJM，有，有、对确定、对确定0)(5 fnfMJM，有有、对对某某些些 )(1fnfMJM，、)()1()(2fnnfnMJMJ 、2、调频波的频谱结构、调频波的频谱结构 包含载波频率分量（但是幅包含载波频率分量（但是幅度小于度小于1，与，与Mf有关。有关。)；还包；还包含无穷多个边频分量；含无穷多个边频分量；各边频分量之间的距离是调各边频分量之间的距离是调制信号角频率制信号

10、角频率 ；各频率分量的幅度由贝塞尔各频率分量的幅度由贝塞尔函数函数 决定；决定；)(fnMJ 奇次旁频分量的相位相反。奇次旁频分量的相位相反。1fM0.770.440.440.110.110.020.02c23 调频波的频谱结构与调制指数调频波的频谱结构与调制指数Mf 关系密切。关系密切。Mf 愈大，则具有一定幅度的边频数目愈多愈大，则具有一定幅度的边频数目愈多。对于某些对于某些Mf值，载频分量或某次边频分量的值，载频分量或某次边频分量的幅度是零。幅度是零。频率调制不是将信号的频谱在频率轴上直接平移频率调制不是将信号的频谱在频率轴上直接平移,而是将信号各频率分量进行非线性变换。因此，频率而是将

11、信号各频率分量进行非线性变换。因此，频率调制又称为非线性调制。调制又称为非线性调制。各频率分量间的功率分配。调频波的功率等于未各频率分量间的功率分配。调频波的功率等于未调载波的功率。调制后，已调波出现许多频率分量，调载波的功率。调制后，已调波出现许多频率分量，这个总功率就分配到各分量。随这个总功率就分配到各分量。随Mf的不同，各频率分的不同，各频率分量之间功率分配的数值不同。量之间功率分配的数值不同。频谱结构特点频谱结构特点3、调频波的频带宽度、调频波的频带宽度调频波的频带宽度有两种近似：忽略小于0.01的分量：（集中99%以上的功率）FMMBWff)1(201.0 忽略小于 0.1的分量：（

12、集中98-99%的功率）)(2)1(21.0FfFMBWmf 卡森（卡森（Carson）公式）公式 理论上，调频波包含有无穷多个频率分量，其带宽是无穷宽的；但实际上，在调制指数一定时，超过某一阶数的贝塞尔函数的值已经相当小，其影响可以忽略，这时则可认为调频波所具有的频带宽度是近似有限的调频波所具有的频带宽度是近似有限的不同不同Mf 时的调频波带宽时的调频波带宽1fMFBWMf2 111.0上式表明，在调制指数较小的情况下，调频波只有角频率分别为 和 的三个分量，它与用同样调制信号进行标准调幅所得调幅波的频带宽度相同。通常，把这种情况的频率调制称为窄带调频。窄带调频。cc1fMmfffBWMM2

13、 11.0上式表明，在调制指数较大的情况下，调频波的带宽等于二倍频偏。通常，把这种情况的频率调制称为宽带调频。宽带调频。又称为恒定带宽调频。恒定带宽调频。介于前两种情况之间。fM)(21.0FfBWm)(21.0FfBWm 恒定带宽调频槪念恒定带宽调频槪念调制指数较大时，调频波的带宽等于二倍频偏。mfBW 21.0 对于调相波，对于调相波，。调相波频带宽度在调制信号频率的高端和低端相差很大，所以对频带的利用是不经济的。mPPVKM 对于调频波，对于调频波，当 减小，增加。mffVkMfM增加，则具有一定幅度的边频数目愈多，带宽增加。带宽增加。减小，则各旁频分量之间的距离减小，带宽减小。带宽减小

14、。fM最大频偏最大频偏mfmVk mpmVk 复杂频率信号的调角信号的频谱复杂频率信号的调角信号的频谱 当两个频率不同的信号同时对一个载波进行频率调制当两个频率不同的信号同时对一个载波进行频率调制时，所得调频波的频谱中，除有载波角频率分量时，所得调频波的频谱中，除有载波角频率分量 及及 和和 分量外，还有分量分量外，还有分量 ,它们是两个调制信号频率之间的组合频率分量。它们是两个调制信号频率之间的组合频率分量。c1nc2kc21kncmaxFF max)(mmff 复杂调角信号频带宽度：复杂调角信号频带宽度：)(21.0FfBWm 调频波的功率调频波的功率个个单单位位。能能量量和和为为表表明明

15、所所有有信信号号频频率率分分量量1 nfnMJ1)(222cmavVP 因此有：因此有：nfncmavMJVP)(222 使振荡器的频率随调制信号成线性关系变化。如：变容二极管直接调频电路。变容二极管直接调频电路。8-2 调频电路调频电路一、调制原理概述一、调制原理概述1、直接调频、直接调频 优点：易于得到比较大的频偏。优点：易于得到比较大的频偏。缺点：中心频率的稳定度不易做得很高。缺点：中心频率的稳定度不易做得很高。2、间接调频、间接调频 优点：载优点：载波中心频率波中心频率稳定度较好稳定度较好)(cos)(0 0 dvktVtvtfccmFM)(cos)(0tvktVtvpccmPM二、调

16、频电路的技术指标二、调频电路的技术指标1、调制特性、调制特性定义：振荡器的频率偏移与调制电压的关系称为调制特性，表示为：)(vgvf 在一定电压范围内，调制特性应近似为直线特性。调制特性应近似为直线特性。2、调制灵敏度、调制灵敏度单位调制电压变化产生的频偏fFvfS在调制电压作用下，所能达到的最大频率偏移。3、最大频偏、最大频偏mfmf f)(tfttvv0004、中心频率稳定度、中心频率稳定度 调频信号的瞬时频率是以稳定的中心频率（载波频率）为基准变化的。如果中心频率不稳定，就有可能使调频信号的频谱落到接收机通带范围之外，以致不能保证正常通信。因此，对于调频电路，不仅因此，对于调频电路，不仅要满足频偏的要求，而且要使中心频率保要满足频偏的要求，而且要使中心频率保持足够高的稳定度。持足够高的稳定度。三、变容二极管直接调频电路三、变容二极管直接调频电路1、变容二极管的特性、变容二极管的特性)1(0BjVvCC PN结反向偏置结反向偏置时，势垒电容随反偏电压改变0VC C0为V=0时变容管的等效电容。为变容指数，大小取决于PN结的结构和杂质分布情况。缓变结变容管，其=1/3；突变结变容管，