02三角形的高、中线与角平分线教案.docx

《02三角形的高、中线与角平分线教案.docx》由会员分享，可在线阅读，更多相关《02三角形的高、中线与角平分线教案.docx（4页珍藏版）》请在第壹文秘上搜索。

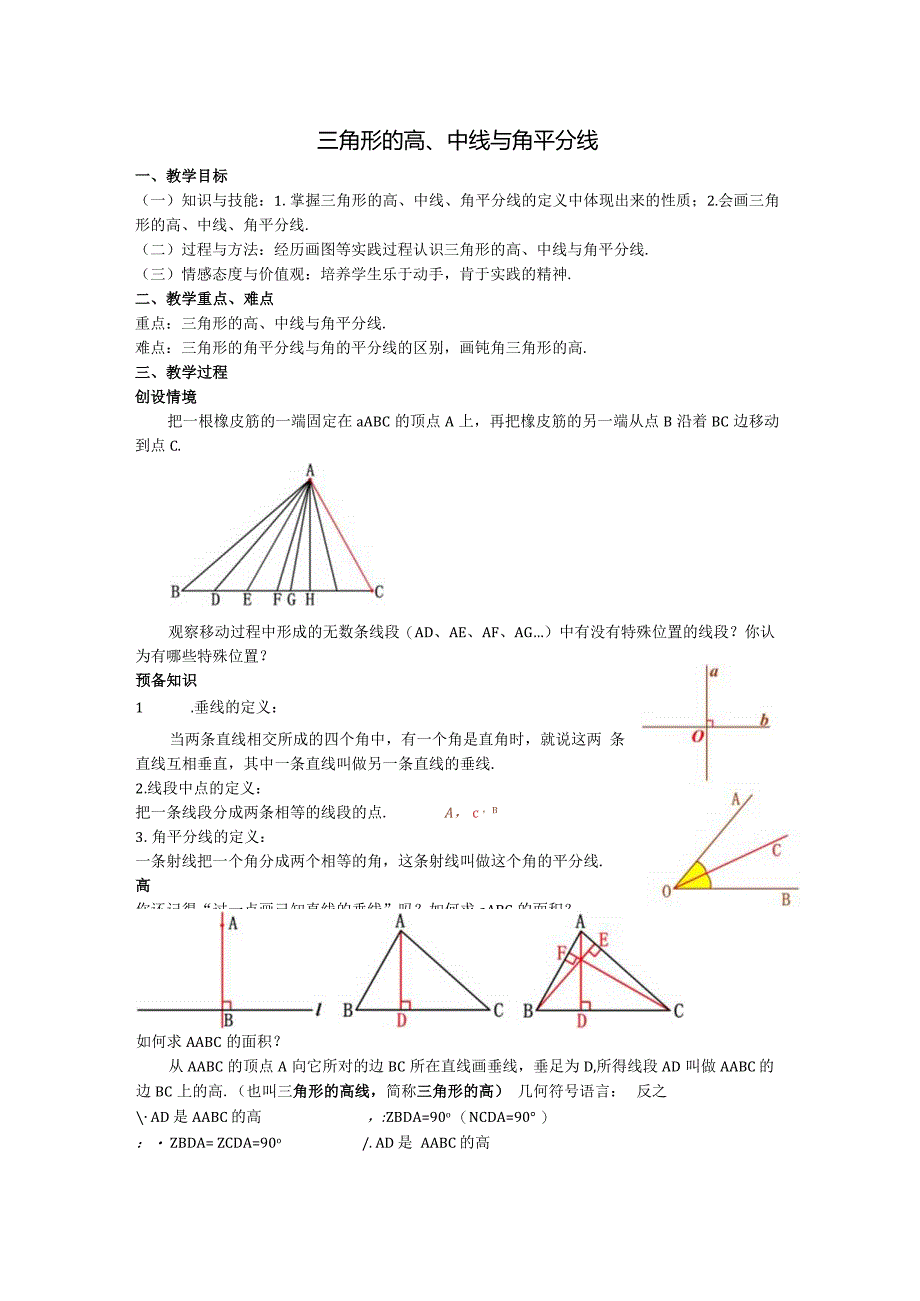
1、三角形的高、中线与角平分线一、教学目标（一）知识与技能：1.掌握三角形的高、中线、角平分线的定义中体现出来的性质；2.会画三角形的高、中线、角平分线.（二）过程与方法：经历画图等实践过程认识三角形的高、中线与角平分线.（三）情感态度与价值观：培养学生乐于动手，肯于实践的精神.二、教学重点、难点重点：三角形的高、中线与角平分线.难点：三角形的角平分线与角的平分线的区别，画钝角三角形的高.三、教学过程创设情境把一根橡皮筋的一端固定在aABC的顶点A上，再把橡皮筋的另一端从点B沿着BC边移动到点C.观察移动过程中形成的无数条线段（AD、AE、AF、AG）中有没有特殊位置的线段？你认为有哪些特殊位置？

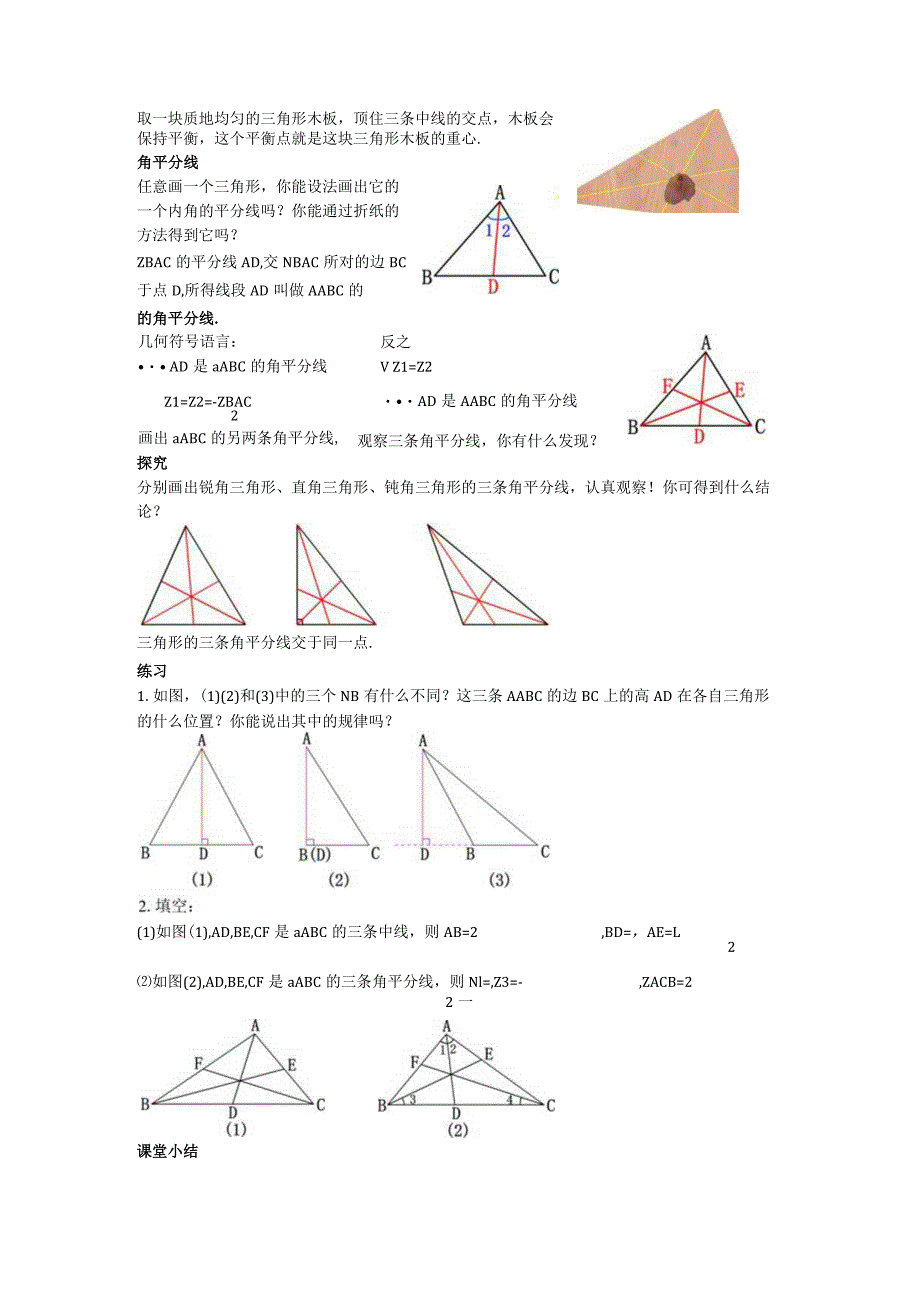
2、预备知识1 .垂线的定义：当两条直线相交所成的四个角中，有一个角是直角时，就说这两 条直线互相垂直，其中一条直线叫做另一条直线的垂线.2 .线段中点的定义：把一条线段分成两条相等的线段的点.A， c ，B3 .角平分线的定义：一条射线把一个角分成两个相等的角，这条射线叫做这个角的平分线. 高你还记得“过一点画己知直线的垂线”吗？如何求aABC的面积？如何求AABC的面积？从AABC的顶点A向它所对的边BC所在直线画垂线，垂足为D,所得线段AD叫做AABC 的边BC上的高.（也叫三角形的高线，简称三角形的高） 几何符号语言：反之 AD 是AABC 的高，:ZBDA=90o （NCDA=90 ）：

3、 ZBDA= ZCDA=90o/. AD 是 AABC 的高用同样的方法你能画出aABC的另两条边上的高吗？你有何发现？锐角三角形的三条高直角三角形的三条高钝角三角形的三条高画出一个锐角三角形，并且画出这个三角形的三条高.这三条高之间有怎样的位置关系？画出一个直角三角形，并且画出这个三角形的三条高.这三条高之间有怎样的位置关系？直角边BC边上的高是；直角边AB边上的高是；斜边AC边上的高是.画出一个钝角三角形，并且画出这个三角形的三条高.这三条高之间有怎样的位置关系？归纳三角形的三条高所在直线交于同一点.思考(中线)已知D是BC的中点，试问AABD的面积与AADC的面积有何关系？连接aABC的

4、顶点A和它所对的边BC的中点D,所得线段AD叫做aABC的边BC上的中线.几何符号语言：反之.AD是AABC的中线,.BD=CD(或BD=BC)2BD=CD=LBCAD是AABC的中线2用同样的方法你能画出aABC的另两条边上的中线吗？你有何发现？探究分别画出锐角三角形、直角三角形、钝角三角形的三条中线,认真观察！你可得到什么结论？三角形的三条中线相交于一点.三角形三条中线的交点叫做三角形的重心.几何符号语言： AD是aABC的角平分线Z1=Z2=-ZBAC2画出aABC的另两条角平分线,反之V Z1=Z2AD是AABC的角平分线观察三条角平分线，你有什么发现？取一块质地均匀的三角形木板，顶住

5、三条中线的交点，木板会保持平衡，这个平衡点就是这块三角形木板的重心.角平分线任意画一个三角形，你能设法画出它的一个内角的平分线吗？你能通过折纸的方法得到它吗？ZBAC的平分线AD,交NBAC所对的边BC于点D,所得线段AD叫做AABC的的角平分线.探究分别画出锐角三角形、直角三角形、钝角三角形的三条角平分线，认真观察！你可得到什么结论？三角形的三条角平分线交于同一点.练习1.如图，(1)(2)和(3)中的三个NB有什么不同？这三条AABC的边BC上的高AD在各自三角形的什么位置？你能说出其中的规律吗？(1)如图(1),AD,BE,CF是aABC的三条中线，则AB=2,BD=，AE=L2如图(2),AD,BE,CF是aABC的三条角平分线，则Nl=,Z3=-,ZACB=22一课堂小结1.本节课你有哪些收获？2.还有没解决的问题吗？四、教学反思本节课由一个动画演示引入,让学生意识到三角形中有很多条特殊的线段.然后从画图入手，分三种情况：即锐角三角形、直角三角形和钝角三角形，培养学生形成分类讨论思想,同时，可以在学生头脑中对这三种线段留下清晰的形象，然后结合这些具体形象叙述它们的定义以及表示方法.