 2023-2024学年湘教版必修第二册4-1-1几类简单几何体1学案.docx
2023-2024学年湘教版必修第二册4-1-1几类简单几何体1学案.docx
《2023-2024学年湘教版必修第二册4-1-1几类简单几何体1学案.docx》由会员分享,可在线阅读,更多相关《2023-2024学年湘教版必修第二册4-1-1几类简单几何体1学案.docx(9页珍藏版)》请在第壹文秘上搜索。
1、4. Ll几类简单几何体(1)教材要点要点一空间几何体1 .空间几何体的定义如果我们只考虑物体的和,而不考虑其他因素,那么由这些物体抽象出来的空间图形称为空间几何体.2 .空间几何体的分类定义由若干个(包括三角形)所围成的封闭体.多面体旋转体把平面上一条封闭曲线内的区域绕着该平面内的一条旋转而成的几何体.图形相关概念轴:定直线称为旋转轴.面:围成多面体的各个多边形;棱:两个面的公共边;顶点:棱和棱的交点.状元随笔(1)任意一个几何体都是由点、线、面构成的.点、线、面是构成几何体的基本元素.我们还可以从运动的观点来理解空间基本图形之间的关系.在几何中,可以把线看成点运动的轨迹,如果点运动的方向始
2、终不变,那么它的轨迹就是一条直线或线段;如果点运动的方向时刻在变化,则运动的轨迹是一条曲线或曲线的一段.同样,一条线运动的轨迹可以是一个面,面运动的轨迹(经过的空间部分)可以形成一个几何体.即点动成线,线动成面,面动成体.(2)多面体与旋转体的异同相同点:两者都是封闭的几何体,包括表面及其内部的所有点.不同点:多面体的表面是平面多边形,旋转体的侧面是曲面,底面为圆.要点二多面体多面体定义图形及表示相关概念特殊几何体棱柱有两个面互相平行,其余各面都是*-8如图可记作:棱柱底面(底):两个互相的面;侧面:其余各面;侧棱:相邻两个侧面的公共边;直棱柱:侧面都是的棱柱;正棱柱:底面是多边形的直棱柱;并
3、且每相邻两个四边形的公共边都互相,由这些面所围成的几何体叫作棱柱.ABCDEF-A,B,C,D,E,F,顶点:侧棱与底面的公共点.长方体:底面和侧面都是矩形的棱柱;正方体:所有棱长都相等的长方体;平行六面体:两个底面是平行四边形的棱柱.棱锥有一个面是多边形,其余各面都是有一个的三角形,这样的几何体叫作棱锥./7株如图可记作:棱锥S-ABCD侧面:具有一个的三角形的面;顶点:这个公共点;侧棱:相邻两个侧面的公共边;底面:除了侧面外,剩下的那一个多边形面.正棱锥:如果棱锥的底面是正多边形,将底面放置后,它的顶点又在过正多边形的铅垂线上.棱台过棱锥任一侧棱上不与侧棱端点重合的一点,作一个与底面的平面
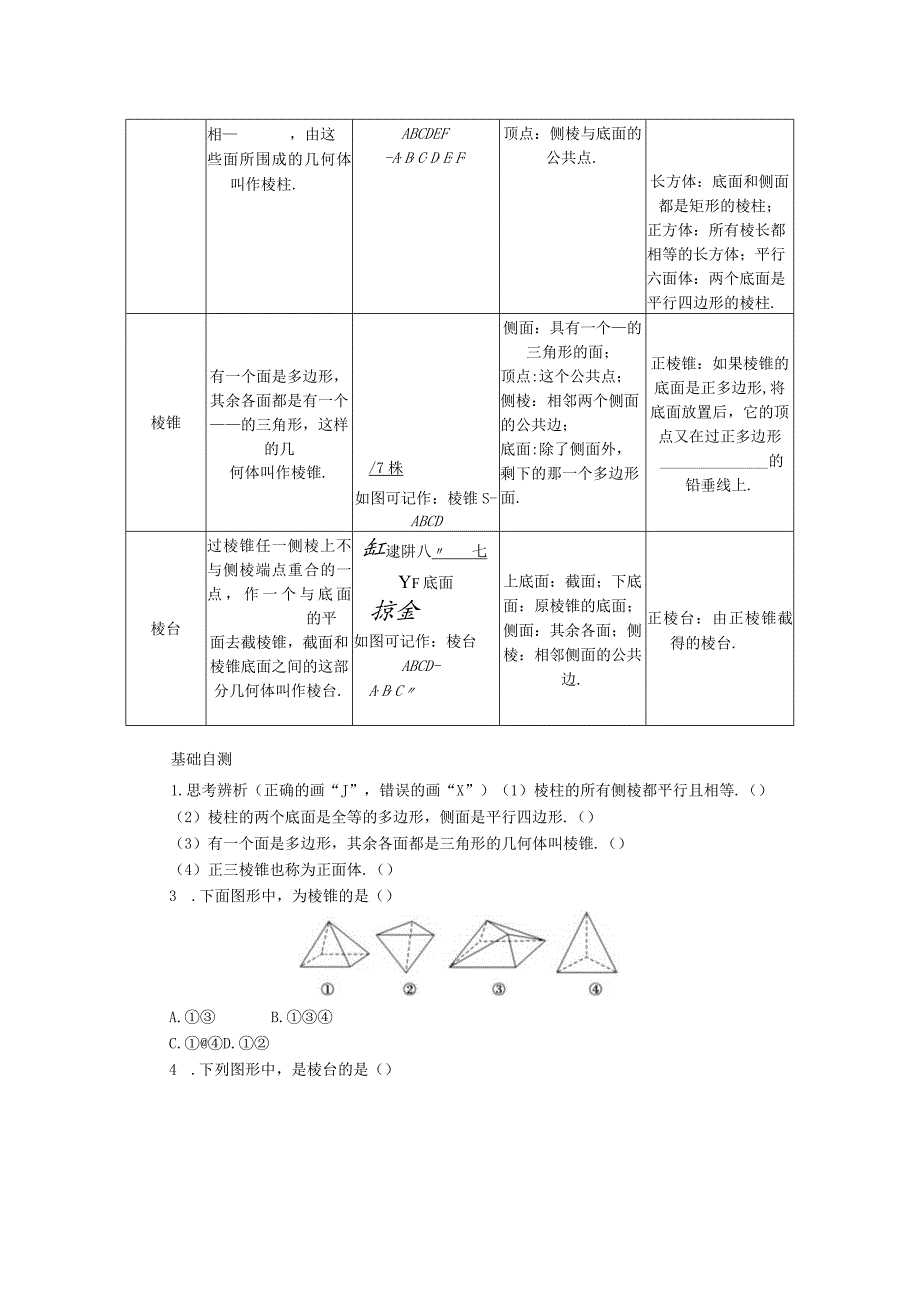
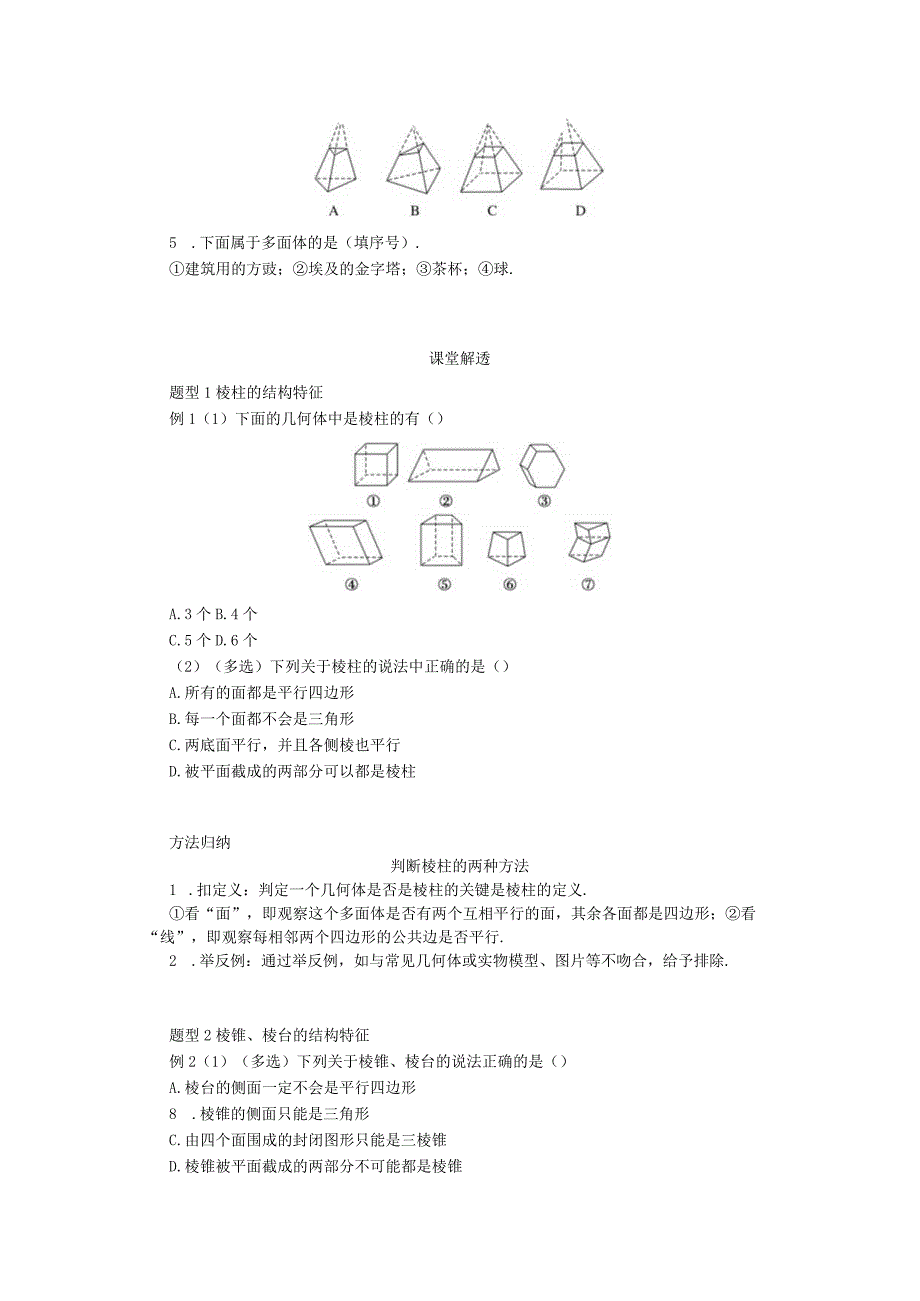
4、去截棱锥,截面和棱锥底面之间的这部分几何体叫作棱台.缸逮阱八七Yf底面掠金如图可记作:棱台ABCD-A,B,C上底面:截面;下底面:原棱锥的底面;侧面:其余各面;侧棱:相邻侧面的公共边.正棱台:由正棱锥截得的棱台.基础自测1.思考辨析(正确的画“J”,错误的画“X”)(1)棱柱的所有侧棱都平行且相等.()(2)棱柱的两个底面是全等的多边形,侧面是平行四边形.()(3)有一个面是多边形,其余各面都是三角形的几何体叫棱锥.()(4)正三棱锥也称为正面体.()3 .下面图形中,为棱锥的是()A.B.C.D.4 .下列图形中,是棱台的是()5 .下面属于多面体的是(填序号).建筑用的方豉;埃及的金字塔
5、;茶杯;球.课堂解透题型1棱柱的结构特征例1(1)下面的几何体中是棱柱的有()A.3个B.4个C.5个D.6个(2)(多选)下列关于棱柱的说法中正确的是()A.所有的面都是平行四边形B.每一个面都不会是三角形C.两底面平行,并且各侧棱也平行D.被平面截成的两部分可以都是棱柱方法归纳判断棱柱的两种方法1 .扣定义:判定一个几何体是否是棱柱的关键是棱柱的定义.看“面”,即观察这个多面体是否有两个互相平行的面,其余各面都是四边形;看“线”,即观察每相邻两个四边形的公共边是否平行.2 .举反例:通过举反例,如与常见几何体或实物模型、图片等不吻合,给予排除.题型2棱锥、棱台的结构特征例2(1)(多选)下
6、列关于棱锥、棱台的说法正确的是()A.棱台的侧面一定不会是平行四边形8 .棱锥的侧面只能是三角形C.由四个面围成的封闭图形只能是三棱锥D.棱锥被平面截成的两部分不可能都是棱锥(2)如图,在三棱台/B,C-4成中,截去三棱锥力-4%,则剩余部分是()A.三棱锥B.四棱锥C.三棱柱D.三棱台方法归纳判断棱锥、棱台形状的两种方法(1)举反例法结合棱锥、棱台的定义举反例直接判断关于棱锥、棱台结构特征的某些说法不正确.(2)直接法棱锥棱台定底面只有一个面是多边形,此面即为底面两个互相平行的面,即为底面看侧棱相交于一点延长后相交于一点题型多面体的平面展开图例3(1)某同学制作了一个对面图案均相同的正方体礼

- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 2023 2024 学年 湘教版 必修 第二 简单 几何体
 第壹文秘所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
第壹文秘所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。


 重点工作绩效评估自评表.docx
重点工作绩效评估自评表.docx
