期末复习06：抛物线限时小练.docx

《期末复习06：抛物线限时小练.docx》由会员分享，可在线阅读，更多相关《期末复习06：抛物线限时小练.docx（8页珍藏版）》请在第壹文秘上搜索。

1、期末复习06：抛物线限时小练（人只要有一种向上的精神，朝若自己的目标一步步努力，成功的机会就会越来越大.是块金子，无论在哪,总是会发光的。）一、单选题1 .若抛物线上x=4y2一点尸到焦点的距离为1,则点P的横坐标是（）A.B.C.0D.216162 .已知抛物线丁=2.武0）的焦点为产，准线为/,过E上的一点A作/的垂线，垂足为AB=3OF（。为坐标原点），且产的面积为12,则E的方程为（）A.y2=4xB.y2-4y3xC.y2=8xD.y2-83x3 .已知抛物线Cy2=2p（po）的焦点为凡准线为/,过点尸且倾斜角为5的直线在第一象限交。于点4若点A在/上的投影为点反且A8=4,则=（

2、）A.1B.2C.22D.44 .已知抛物线C=8x,过点尸（2,T）的直线/与抛物线C交于A,B两点、,若AP=BPt则直线/的斜率是（）A.-4B.4C.-D.-44二、多选题5 .已知直线/：y=x+m过抛物线CV=4的焦点尸，且与抛物线交于A,B两点，则（）A. in=IB. AB=8C. AF=2BFD.抛物线C上的动点到直线y=x+2距离的最小值为正26 .在平面直角坐标系中，已知尸（2,0）,过点F可作直线/与曲线C交于“，N两点，使IMNI=2,则曲线C可以是（）A.y2=8xB.-=1627 .已知直线/过抛物线E:V=4X的焦点产，与抛物线相交于A(,y)6(勺,%)两点，

3、分别过AB作抛物线的准线4的垂线,垂足分别为A，g,以线段A4为直径作圆MQ为坐标原点，下列正确的判断有()A.xy+x22B.二AOB为钝角三角形C.点尸在圆M外部D.直线A尸平分NOEA8 .己知抛物线C：x2=2py(0)的焦点为尸，。为抛物线C上一动点，设直线/与抛物线C相交于A,8两点，点”(2,2)不在抛物线。上()A.若直线/过点M,F且与轴垂直，则P=48 .若PM+PF的最小值为3,则P=2C.若直线/经过焦点尸，则直线OB(0为坐标原点)的斜率心”8满足l0A,c0B=D.若过A,B所作的抛物线。的两条切线互相垂直，且A,8两点的纵坐标之和的最小值为2,则Si=2三、填空题

4、9 .已知抛物线C：V=2p(p0)的焦点为尸，点争)(0)在C上，IAFI=5,若直线AF与C交于另一点3,则忸目的值为.10 .已知抛物线C：x2=4y的焦点为7,4(3,4),P为C上一点,则4+P尸|的最小值为.11 .已知过点(多O)(P0)的直线与抛物线Uy2=2px交于AB两点，若IA例=3p且线段AA的中点的横坐标为1,则C的方程为.12 .己知双曲线C:(卫=1(0,。0)的左顶点与抛物线V=22氏50)的焦点的ab距离为6,且双曲线的一条渐近线与抛物线的准线的交点坐标为(-3,-2),则双曲线的焦距为.参考答案：1. A【分析】将抛物线方程化为标准形式，根据焦半径公式得到方

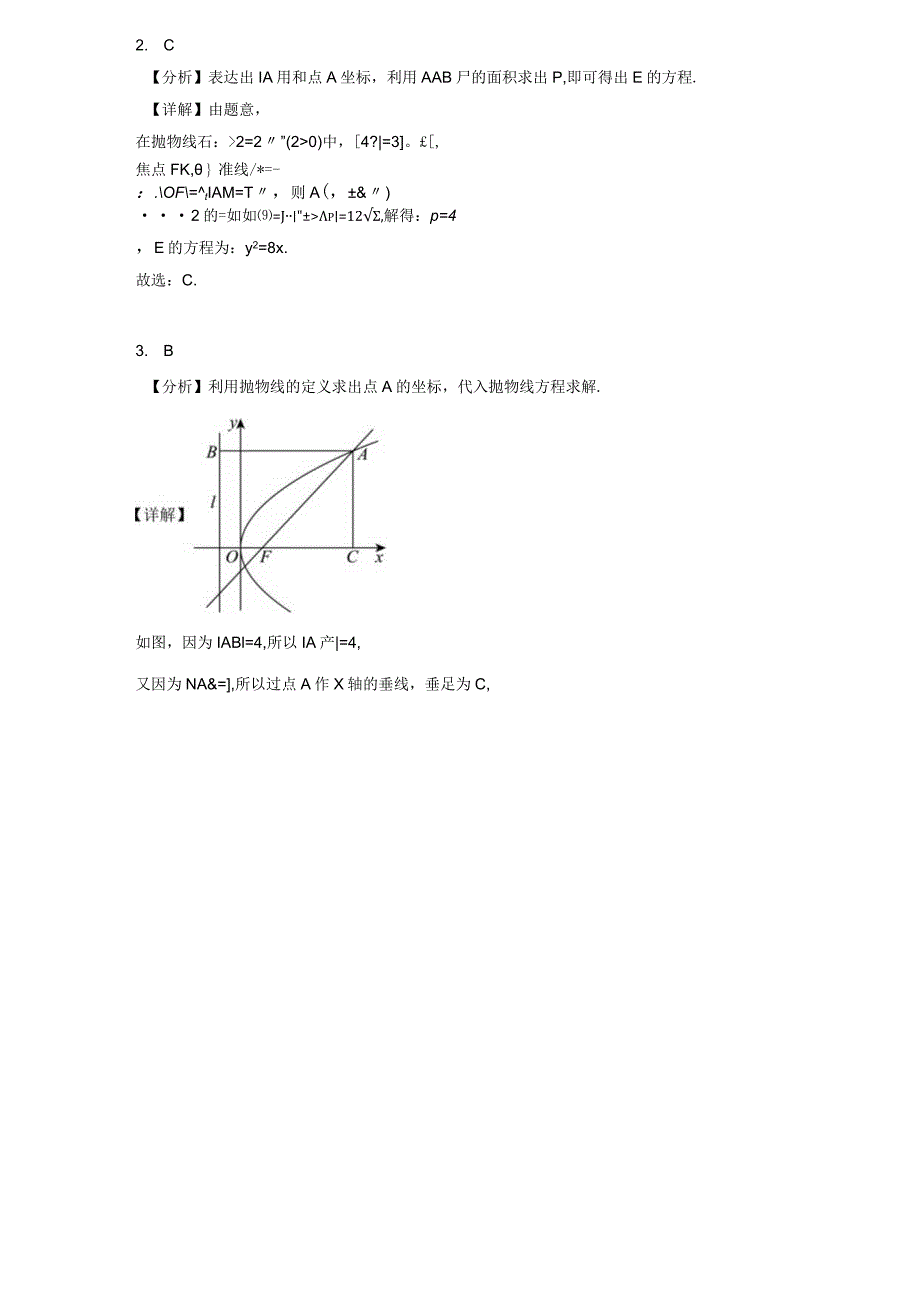
5、程，求出答案.【详解】1=4/化为标准形式为、2=4，故焦点坐标为但,01，准线方程为x=4116)16由焦半径可得/+=1,解得/=裳IoIo故选：A2. C【分析】表达出IA用和点A坐标，利用AAB尸的面积求出P,即可得出E的方程.【详解】由题意，在抛物线石：2=2”(20)中，4?|=3。,焦点FK,准线/*=-：.OF=tIAM=T，则A(，&)2的=如如=Jp=12,解得：p=4，E的方程为：y2=8x.故选：C.3. B【分析】利用抛物线的定义求出点A的坐标，代入抛物线方程求解.如图，因为IABl=4,所以IA产|=4,又因为NA&=,所以过点A作X轴的垂线，垂足为C,则I产CI=

6、ZIAq=2后所以4(2+23),因为点A(2+23)在抛物线上，所以12=2x(2+5),整理得，p2+4p-12=0,解得p=2或p=-6(舍)，故选:B.4. A【分析】利用点差法求解即可.【详解】设Aa,y),B(再,力)，则二作差得y；-y=8（内-w）.因为IAH=BP,所）,2=芯x2，以尸是线段AB的中点，所以乂+必=-2,则直线/的斜率Z=M=号r-4故选：A5. BD【分析】求得抛物线C的焦点代入直线/的方程，求得m=T,可判定A错误；联立方程组,根据韦达定理和抛物线的焦点弦的性质，求得IM=8,可判定B正确；结合抛物线的定义,求得|明,忸目的值，可判定C错误；设设M(Ky

7、)是抛物线C上的任意一点，利用点到直线的距离公式，结合二次函数的性质，可判定D正确.【详解】由抛物线Uy?=,可得焦点为尸(1,0),因为/:y=x+m过抛物线C的焦点F,可得6+1=0,解得m=-1,所以A错误；联立方程组y = X-I y2 =4x整理得f-6x + l=0,设A(X,凹),802，%)，则A=36-4=32(),x1+x2=6,x1x2=1,由抛物线的焦点弦的性质，可得卜同=玉+=6+2=8,所以B正确；又由x2-6x+l=0,解得芭=3+2正,占=3-2应，根据抛物线的定义，可得IAFI=X14=4+22叫=2(x2+9=8-42,所以IAqW2忸耳，所以C错误；设M(

8、,y)是抛物线C上的任意一点，可得y12=4x,则点M到直线y=x+2的距离为,_后一乂+2|_(%一2)2+4,d=/2=-忑-=42当y=2时，Jmin=,所以D正确.故选：BD.6. BCD【分析】根据题意得到点尸为四个曲线的焦点，结合椭圆、双曲线和抛物线的焦点弦的性质，逐项判定，即可求解.【详解】由题意，根据选项可得，点F恰为四个曲线的焦点，A中，抛物线y2=8x焦点弦弦长最小值为2p=8,故不存在弦长IMNl=2,所以A不正确;I中，根据椭圆的性质，可得焦点弦弦长取值范围为即2券，2#,而2e,2,所以B正确;因为2e所以C正确;即岸),C中，若M,N同在右支上，则焦点弦弦长取值范围

9、为,+(D中，若M,N在异支上，则焦点弦弦长取值范围为24,+oo),即2,go),因为22,+s),所以D正确.故选：BCD.7. ABD【分析】对选项A,根据焦半径公式即可判断A正确，对选项B,根据。403=-30即可判断B正确，对选项C,D,根据抛物线的性质得到卬产=NoR=ZAFAy,AAyFBx=90。，即可判断C错误，D正确.【详解】如图所示：对选项A,由抛物线的焦半径公式可知IAM=不+%+22=4,所以+z2,故A正确；对于选项B,OAO8w+yy2=（；?+PM，令直线/的方程为X=+1,代入y2=4得）,2_4m），-4=0,所以升%=-4，所以QAO4=-3vO,所以08

10、是钝角三角形，故B正确；对选项C,D,由IAAII=IAFl可知NM尸=NAE4l,又ZoF、所以NAA/=NoR=NAR,所以直线平分角NAFO,同理可得尸8平分角N班O,所以A尸，与尸，即NA尸g=90。，所以圆”经过点尸，故C错误，D正确.故选：ABD8. ACD【分析】对于A,根据=2求出=4,可知A正确；对于B,当点M在抛物线C的外部时，求出=4+24，可知B不正确；对于C,利用斜率公式计算可得勺XOB=-；，可知C正确；对于D,设Aa,y）,B（x2,y2）,利用两条切线互相垂直求出XX2=-P=根据y+%的最小值，得到A8的坐标，再求出三角形A三的面积，可知D正确.【详解】若直线

11、/过点M,/且与）轴垂直，则与二2,所以=4,所以A正确.当点M在抛物线C的内部时，设/是抛物线的准线，过点尸作/WJJ于点N,则IPMl+PFHPM+PN2+4,当且仅当P,MtN三点共线时等号成立，所以2IPMl+PF的最小值是2+4，由2+g=3得p=2；22当点M在抛物线C的外部时，连接“/，则IPMl+PF的最值为M11,所以IMFI=JfK21+22=3,得p=4+2币,所以B不正确.易知直线/的斜率存在，设直线/：y=kx+,与=2p),联立,消去y得/-2p丘-p2=0,设Aa,yj,B(x29y2)t则MX2=-/,从而可得,必=与乎=f,所以bAkOB=迎*=-；,所以C正

12、确.XIX2q设A(X1,),B(x2,y2)f由犬=2py得=所以后也8=亍V2=T,即内=-p2,所以y+必=B(X：+用=已(占+%-2中2=/(X+/F+p,所以当x+%=o时，)i+y?取得最小值，且(y+%)min=p=2,V24所以为=7：2，所以(一12)2=一，=4，即W=2,y2=T2-=T-T7=1,2p22因为点M(2,2),所以治加二卜4乂1=2,所以D正确.故选：ACD.【点睛】关键点点睛：掌握抛物线的标准方程和几何性质是解题关键.9. /7.5/7-22【分析】由焦半径公式得到方程，求出P=6,得到V=12,(2,26),尸(3,0),从而得到故直线AF方程，联立

13、抛物线方程，求出8点横坐标，由焦半径求出答案.【详解】由焦半径公式得IAPl=O+5=5,所以二6；故.y2=12x,（2,26）,F（3,）,V-0JV3L故直线AF方程为年后=33，即=-26（工-3）,联立丁=12x与y=-2的X-3）得6/一39x+54=O,99解得%=2,N=,故8点横坐标为所以I叫二卜与=卜3=泉112222故答案为：y10. 5【分析】根据抛物线的定义求得正确答案.【详解】过尸作准线的垂线，垂足为8,!HJ4+PF=4+PB,显然点P在抛物线内，则当P,A,8三点共线时，|/川+|冏最小，其最小值为4+1=5.11. =2x【分析】根据抛物线的定义、弦长公式列方

14、程，求得，进而求得抛物线的方程.【详解】点（多0）是抛物线Uy2=2PX的焦点，则直线A8过抛物线的焦点，设Aa,y）,8（再,3），则X+%2=2x1=2,贝|明=%+毛+=2+=3,=1,所以抛物线的方程为V=2儿故答案为：y2=2x【分析】依题意可得抛物线的准线为=-3,即可求出/，从而求出明再由渐近线方程求出6,即可求出J【详解】依题意可得抛物线的准线方程为JV=-3,W-=-3,所以=6,则抛物线的焦点为(3,0),则双曲线的左顶点为(-3,0),即=3,由双曲线的一条渐近线为y=x,又双曲线的渐近线方程为y=2,所以力=2,则C=行方=Ji3，所以双曲线的焦距为2jB故答案为：2?