几何培优讲义 三角形 手拉手模型.docx

《几何培优讲义 三角形 手拉手模型.docx》由会员分享，可在线阅读，更多相关《几何培优讲义 三角形 手拉手模型.docx（8页珍藏版）》请在第壹文秘上搜索。

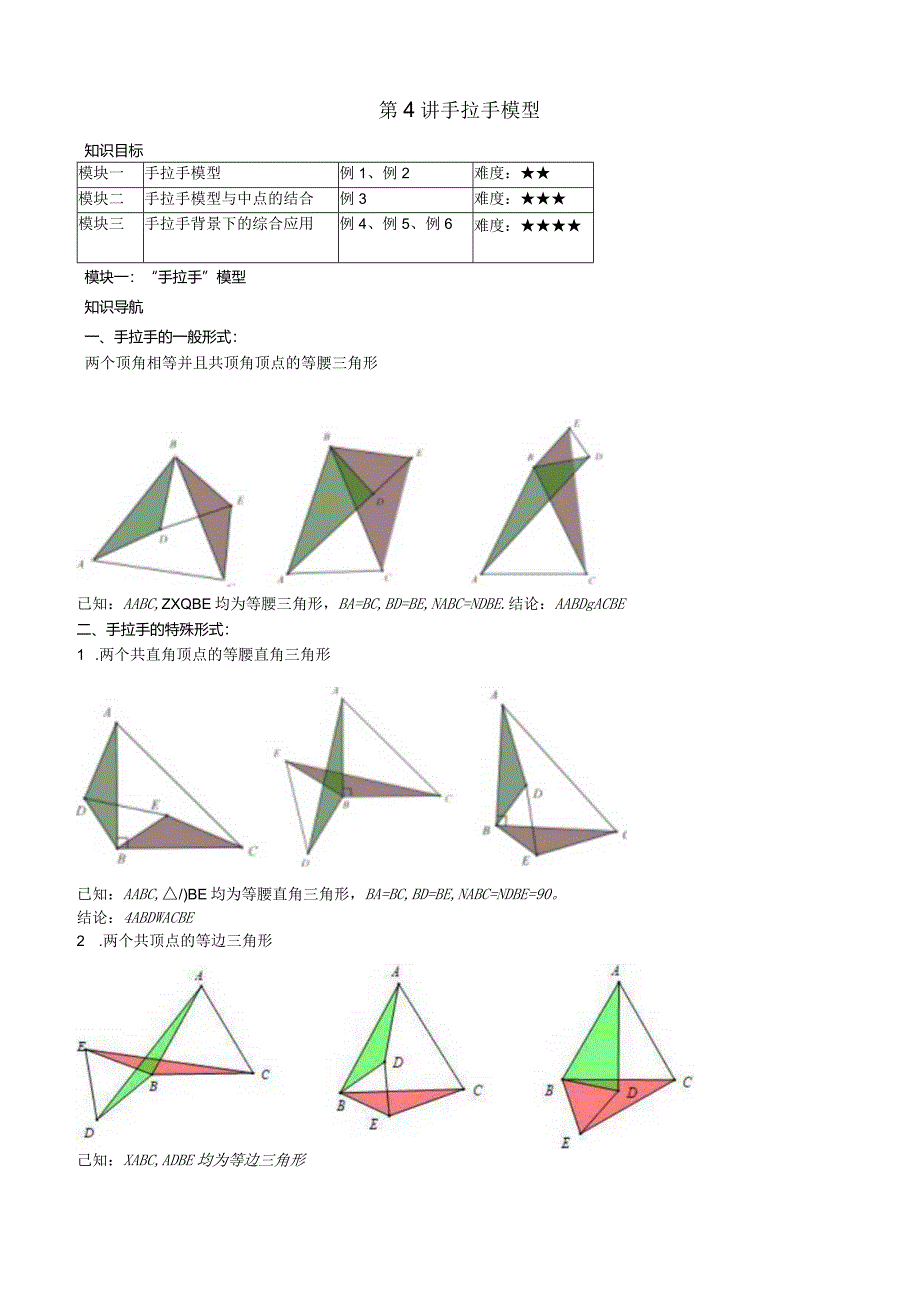
1、第4讲手拉手模型知识目标模块一手拉手模型例1、例2难度：模块二手拉手模型与中点的结合例3难度：模块三手拉手背景下的综合应用例4、例5、例6难度：模块一：“手拉手”模型知识导航一、手拉手的一般形式：两个顶角相等并且共顶角顶点的等腰三角形已知：AABC,ZXQBE均为等腰三角形，BA=BC,BD=BE,NABC=NDBE.结论：AABDgACBE二、手拉手的特殊形式：1 .两个共直角顶点的等腰直角三角形已知：AABC,/)BE均为等腰直角三角形，BA=BC,BD=BE,NABC=NDBE=90。结论：4ABDWACBE2 .两个共顶点的等边三角形己知：XABC,ADBE均为等边三角形结论：LABD

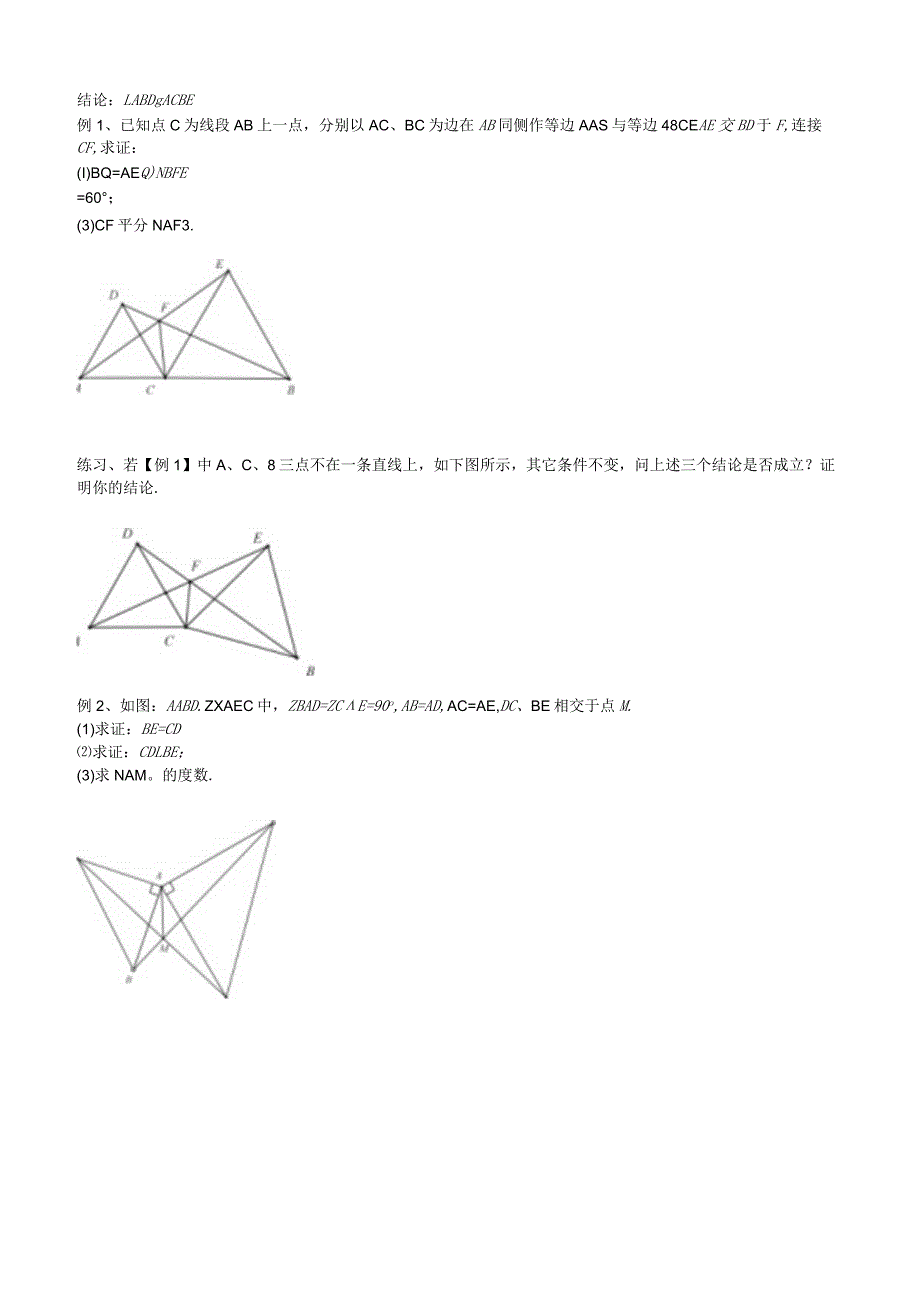
2、gACBE例1、已知点C为线段AB上一点，分别以AC、BC为边在AB同侧作等边AAS与等边48CEAE交BD于F,连接CF,求证：(I)BQ=AEQ)NBFE=60；(3)CF平分NAF3.练习、若【例1】中A、C、8三点不在一条直线上，如下图所示，其它条件不变，问上述三个结论是否成立？证明你的结论.例2、如图：AABD.ZXAEC中，ZBAD=ZCE=90o,AB=AD,AC=AE,DC、BE相交于点M.(1)求证：BE=CD求证：CDLBE；(3)求NAM。的度数.练习、如图，已知直线A8交X轴于点A3，0)，交y轴于点B(0,b),且,bjz+()2=O若点C在第一象限，且8EJ_AC于

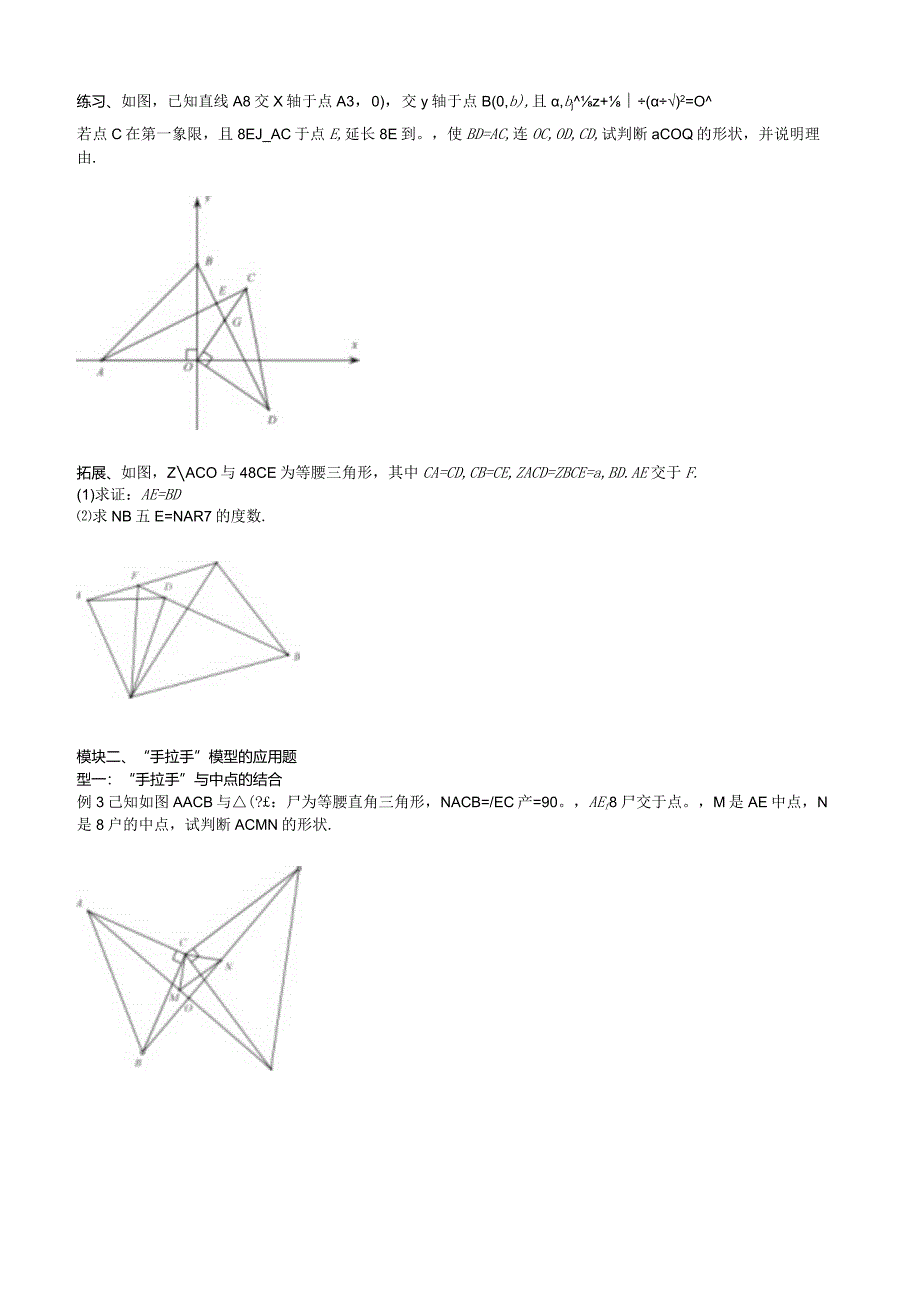
3、点E,延长8E到。，使BD=AC,连OC,OD,CD,试判断aCOQ的形状，并说明理由.拓展、如图，ZACO与48CE为等腰三角形，其中CA=CD,CB=CE,ZACD=ZBCE=a,BD.AE交于F.(1)求证：AE=BD求NB五E=NAR7的度数.模块二、“手拉手”模型的应用题型一：“手拉手”与中点的结合例3己知如图AACB与(?：尸为等腰直角三角形，NACB=/EC产=90。，AEf8尸交于点。，M是AE中点，N是8户的中点，试判断ACMN的形状.练习、已知AABC,分别以A8,AC为边作AABO和AACO,KAD=ABfAC=AEfZDAB=ZCAE,连接OC与BE,G,尸分别是QC与

4、BE的中点.(1)如图，若NoAB=60。，则NA尸G=.(2)如图，若NDAB=a,则试探究NA尸G与之间的关系.模型三、“手拉手”背景下的综合应用例4如图，设AAOC和ACBE都是等边三角形，连接AE、AB.BD,ZABD=80of求NEAB的度数.练习、如图，设AABC和E都是等边三角形，且NE8Q=65。，求N4EB的度数.例5、如图，是等边三角形，以直线OA为X轴建立平面直角坐标系，B(a,勿且,b满足，。为y轴上移动点，以A。为边做等边aAOC直线CB交)，轴于点E.(1)如图1,求A点的坐标(2)如图2,。在)，轴正半轴上，C在第二象限，CE的延长线交X轴于点M,当。点在y轴正半

5、轴上运动时,M点的坐标是否发生变化，若不变，求M点的坐标，若变化，说明理由.例6、4AOB和AACO是等边三角形，其中LX轴于E点,(1)如图，若OC=5,求8。的长度设BD交X轴于点F,求证：ZOFA=ZDF.(3)如图，若正ZXAOB的边长为4,点。为K轴上一动点，以AC为边在直线AC下方作正aACD,连接OE,求OE的最小值.限3第4讲本讲课后作业1 .如图，等边4ABC,。是AB边上动点，以Co为边，向上作等边aEQC,连AE.求证：AE/BC.(2)若。点运动到BA延长线上，其它条件不变，是否仍有AE/BC?2 .(1)如图1,ZXABC和AECD都是等边三角形，图中有一对全等三角形

6、可以看成是旋转变换得到的，它们是;(2)在(1)中，将绕。点任意旋转一个角度得如图2,分别取A。、BE的中点M、N,连接MN、MC、NC,请判断AMCN的形状，并证明你的结论.3 .如图，已知aABC是等边三角形，点E在线段AB上，点。在射线CB上，且。E=CE,以CE为边等边三角形CEF,连接EF.(1)求证：BE=AF.(2)猜想线段AB、DB、A尸之间的数量关系，并证明你的猜想.4 .如图，设AABC和都是等边三角形，若NAE8=70。，求NEBO的度数.5 .如图，ZXABC为等腰直角三角形，其中A8=AC,NBAC=90。，点A、。在BC的异侧且NBOC=90。,连接AD,过点A作AEYAD交DB延长线于点E,求NE的度数.6 .如图1,在AABC中，ZA=360,AB=ACfNABC的平分线BE交AC于E.(1)求证：AE=BC(2)如图2,过点E作E尸BC交A8于尸，将?!：尸绕点A逆时针旋转角1(0。144。)得到力户。连接