 构造全等三角形的基本方法.docx
构造全等三角形的基本方法.docx
《构造全等三角形的基本方法.docx》由会员分享,可在线阅读,更多相关《构造全等三角形的基本方法.docx(4页珍藏版)》请在第壹文秘上搜索。
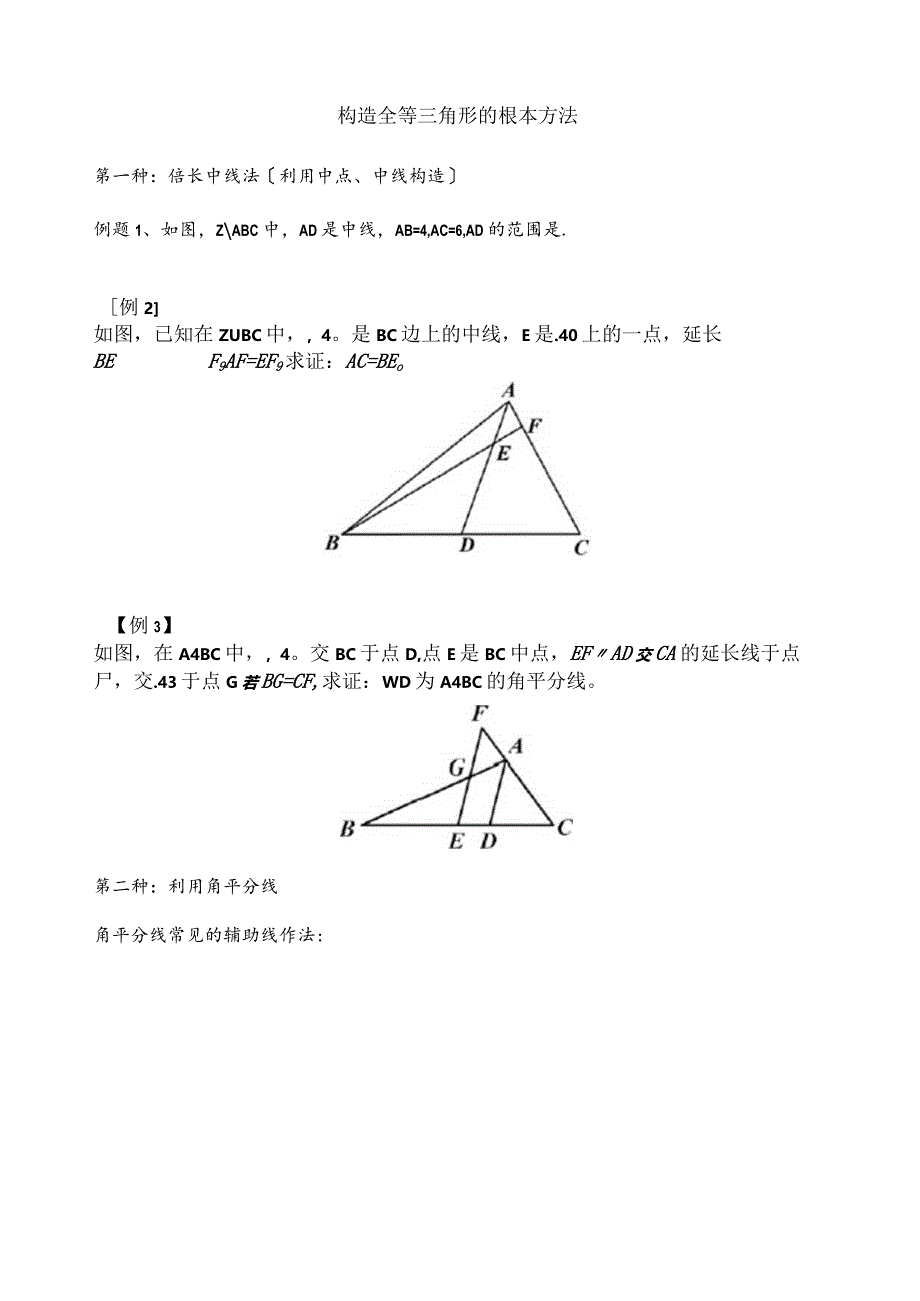
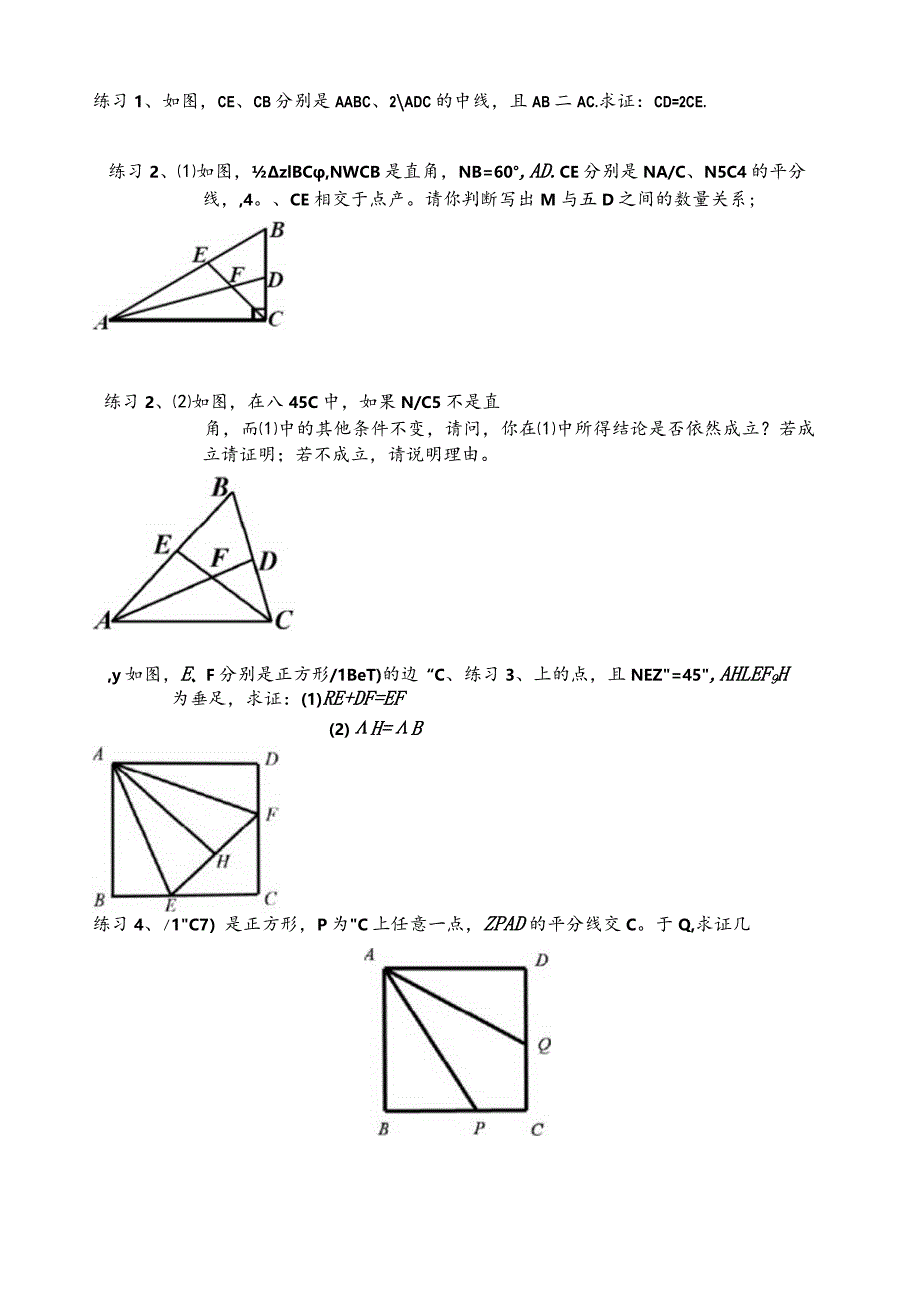
1、构造全等三角形的根本方法第一种:倍长中线法利用中点、中线构造例题1、如图,ZABC中,AD是中线,AB=4,AC=6,AD的范围是.例2如图,已知在ZUBC中,4。是BC边上的中线,E是.40上的一点,延长BEF9AF=EF9求证:AC=BEo【例3】如图,在A4BC中,4。交BC于点D,点E是BC中点,EFAD交CA的延长线于点尸,交.43于点G若BG=CF,求证:WD为A4BC的角平分线。第二种:利用角平分线角平分线常见的辅助线作法:I【例1】I:NI=N2,Z3=Z4,来证:.4P平分NA4C.例题2、在AABC中,ZB=2ZC,NA的平分线AD交BC边于点D.求证:AC=AB+BD.例
2、题3、BE是角平分线,AD垂直BE于D,求证:Z2=Z1+ZC第三种:截长补短法通常用来证明线段和差相等“截长法”即把结论中最大的线段根据条件分成两段,使其中一段与较短线段相等,然后证明余下的线段与另一条线段相等的方法.“补短法”为把两条线段中的一条接长成为一条长线段,然后证明接成的线段与较长的线段相等,或是把一条较短的线段加长,使它等于较长的一段,然后证明加长的那局部与另一较短的线段相等.例题5:如图1:正方形ABCD中,NBAC的平分线交BC于E,求证:AB+BE=AC.例题6、ABCD,BE,CE是角平分线,求证:BC=AB+CD第四种:旋转对题目中出现有一个公共端点的相等线段时,可试用

- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 构造 全等 三角形 基本 方法
 第壹文秘所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
第壹文秘所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。


 重点工作绩效评估自评表.docx
重点工作绩效评估自评表.docx
 大班语言《十二生肖》PPT课件教案PPT课件.pptx
大班语言《十二生肖》PPT课件教案PPT课件.pptx
