第23讲函数y＝Asin(ωx＋φ)的图象及应用（讲）（教师版）.docx

《第23讲函数y＝Asin(ωx＋φ)的图象及应用（讲）（教师版）.docx》由会员分享，可在线阅读，更多相关《第23讲函数y＝Asin(ωx＋φ)的图象及应用（讲）（教师版）.docx（19页珍藏版）》请在第壹文秘上搜索。

1、第23讲函数y=Asin(x+)的图象及应用(讲)思维导图题型1:“五点法作图及图象变换题型2:求函数y=Asin(3x+)89W析式考向1:三角函数性质的综合问题函数y = Asin(x + )的图象及应用题型3:三角函数图象与性质的综合问题(考向2:三角函数的实际应用I考向3:函数零点(方程根)f最横坐标伸缩与3的关系不清致误常见误区/图象平移与9的关系不清致误I确定不了解析式中的值致误知识梳理1 .函数y=Asin(s+g)的有关概念y=sin(x)(A0,0)振幅周期频率相位初相AT2T=f=L=处jT2x+(p2 .用五点法画y=Asin(cx+9)(A0,cO)一个周期内的简图用五

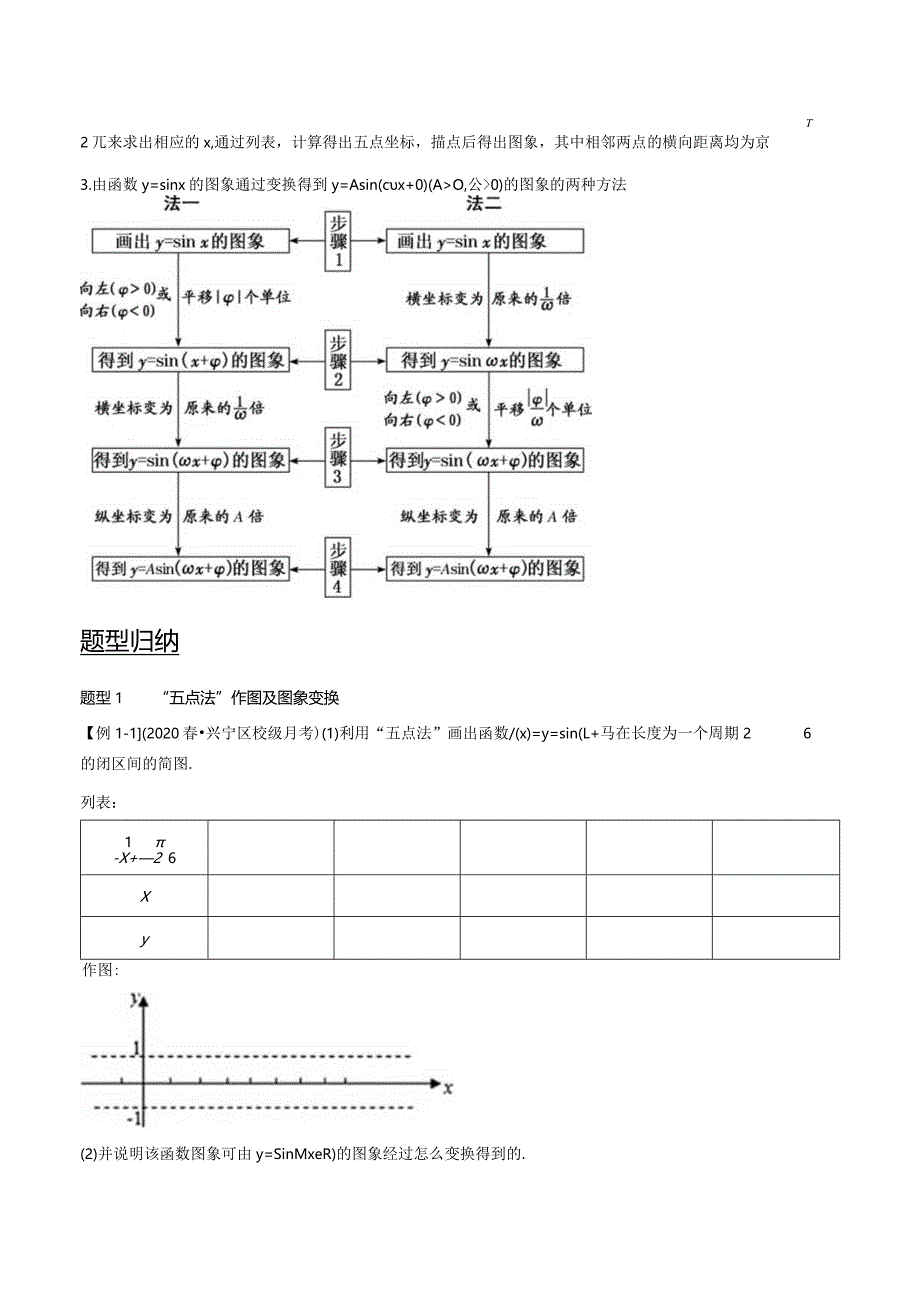
2、点法画y=Asin(3r+3)(AO,m0)一个周期内的简图时，要找五个关键点，如下表所示:-023T2X-2L_2-0红一幺22-0y=Asin(cx+0)0A0-0五点法作图的步骤用“五点法”作函数y=4sin(sx+p)的简图，精髓是通过变量代换，设z=(x+%由Z取0,看,y,T2兀来求出相应的x,通过列表，计算得出五点坐标，描点后得出图象，其中相邻两点的横向距离均为京3.由函数y=sinx的图象通过变换得到y=Asin(cx+0)(AO,公0)的图象的两种方法题型归纳题型1“五点法”作图及图象变换【例1-1(2020春兴宁区校级月考)(1)利用“五点法”画出函数/(x)=y=sin(

3、L+马在长度为一个周期26的闭区间的简图.列表：1-X+26Xy作图:(2)并说明该函数图象可由y=SinMxeR)的图象经过怎么变换得到的.(3)求函数f(x)图象的对称轴方程.【分析】(1)按照“五点法”画出函数图象的步骤：列表、描点、连线，画图即可;(2)经过平移变换和伸缩变换即可得到函数的图象.(3)由L+工=区+三，Z,即可解得函数的对称轴方程.262【解答】解：(1)先列表，后描点并画图1X+26023T2X32T5T8兀Ty010-10(2)把y=sinx的图象上所有的点向左平移巴个单位，再把所得图象的点的横坐标伸长到原来的2倍(纵6坐标不变)，得到y=sin(L+马的图象，即y

4、=Sindx+马的图象；2626(3)由x+匹=&+三，可得X=2k,AreZ,2623所以函数的对称轴方程是x=2M+空，keZ.3【例1-2】(2020春安徽期末)要得到函数y=cosx+马的图象，只需将函数y=cosx-马的图象()2326A.向左平移巴个单位长度B.向右平移上个单位长度2 2C.向左平移1个单位长度D.向右平移1个单位长度【分析】由题意利用函数y=Acos(3x+q)的图象变换规律，得出结论.【解答】解：把函数y=cos(Xq)=COs/(x-g)的图象向左平移1个单位长度,可得函数y=8s(x-g+l)=cos(x+g的图象的图象，故选：C.【跟踪训I练I-1(202

5、0春云南期末)函数y=sin2w(G0)的图象向左平移2个单位长度，所得图象关于6y轴对称，则口的一个可能取值是()3 21A.2B.-C.-D.-232【分析】由题意根据函数y=Asin(s+)的图象变换规律，三角函数的图象的对称性，得出结论.【解答】解：把函数y=sin2(y(0)的图象向左平移工个单位长度，6可得y=sin(2ox+)的图象，根据所得图象关于y轴对称，可得竺=%乃+2,Z,32则切的个可能取值为3,2故选：B.【跟踪训练1-2】(2020春广州期末)已知函数f(x)=sinx,g(x)=sin(2x+马,将/(力的图象经过下列哪种变换可以与g(x)的图象重合()A.向左平

6、移工个单位，6再把各点的横坐标缩短到原来的!2B.向左平移立个单位,12再把各点的横坐标缩短到原来的L2C.向左平移工个单位，6再把各点的横坐标伸长到原来的2倍D.向左平移立个单位,12再把各点的横坐标伸长到原来的2倍【分析】直接利用函数的图象的平移变换和伸缩变换的应用求出结果.【解答】解：将函数/(幻=SinX的图象向左平移工个单位，再将函数上各点的横坐标缩短为原来的工，得62至IJg(x)=sin(2x+工)的图象.故选：A.【跟踪训练1-3】(2019秋道里区校级期末)已知函数/(x)=2COSX(由SinX+cosx)-l.(I)求函数/(X)的最小正周期并用五点作图法画出函数y=(x

7、)在区间0,划上的图象;（三）若将函数/a)的图象向右平移工个单位长度，得到函数以外的图象，求函数g(x)的解析式，并求当63哈争时，函数g(x)的最小值及此时的X值.【分析】(I)利用三角恒等变换化简函数的解析式，再利用五点法作图，画出函数/(X)在0,幻上的图象.（三）利用函数y=Asin(ox+e)的图象变换规律，求得g(x)的解析式，再利用正弦函数的定义域和值域，即可得解.【解答】解：(I)/(x)=2cosx(3sinx+cosx)-1=3sin2x+1+cos2x-=2sin(2x+),6.函数f(x)的最小正周期T=等=%，在0,划上，2x+-,666列表如下：函数F(X)在区间

8、0,%上的图象是:C低2x+-677342213乃6X05n2Tny120-201作图如下:(II)将函数f(力的图象向右平移三个单位长度,得到函数g(x)=2sin(2x三)的图象,66I-T-r7T24-lli.人7VrTC7TC.由J-X,时，2,9123636故当2x-时，即X=-C时，函数取得最小值为2sin(-2)=-L63123【名师指导】(1)，=ASin(S:+的图象可用“五点法”作简图得到，可通过变量代换Z=S+e计算五点坐标.(2)由y=sin5到y=sin(cux+e)的变换：向左平移为(00,卬0)个单位长度而非p个单位长度.(3)平移前后两个三角函数的名称如果不一致

9、，应先利用诱导公式化为同名函数，G为负时应先变成正值.题型2求函数y=Asin(x+)的解析式【例2-1】(2020新乡二模)如图，P,Q是函数/(x)=ACOS(5+*)(AO,00,-%0,0时，由/(一g)=3,可得9=2攵万+得，左Z,结合/v,此时9取不到符合题意的值；当。VO时，由一|)=3,解得夕需，左Z;结合|在苫，可得Z=T时，=J即可得解.10【解答】解：由函数y=Asin(3x+)+B的部分图象知，A+B=3-A+ = O解得A = B = -X 2又?妥咛=小解得T=年;所以IO时，函数的解析式为y=sin(x+8)+T,i冗、3.6/万、3C乂/(-y)=-SlnqX

10、(-)+)+-=3,sin(一等+0)=1,一等+=2k+，ksZ：解得0=22万+得，Z;又|如,此时e取不到符合题意的值；(2)当3V0时，函数的解析式为y=-Tsinfx-e)+,乂/(一A)=-ISin(SX(-5)一夕)+=3,sin(一:一*)=一1,2=2k+,左Z;解得*=一24万一筹.AZ;父网,可得A=-1时，=-,10综上，Q的值为a故选：A.【跟踪训练2-1】(2020春新余期末)已知函数/(x)=ASiI1(次+夕)(40,0,/g)的部分图象如图【分析】由函数/(X)的部分图象求得A、T、G和。的值，即可写出/(x),进而根据特殊角的三角函数值即可求解.【解答】解：

11、由函数/(x)=ASin(5+)的部分图象知，A=2,Ir=-,解得7=4万=空，2331.=-;2又/(争=2sin(gX1+。)=2，可得工X至+/=24乃+至，左Z,ft?W=2k+,左Z,2326,0,G0,的部分图象如图所示,将函数/*)的图象向右平移上个单位后，所得到的图象对应的函数为(A.y=2sin(2x-y)B.y=2sin(gx-g)C.y=2sin(2x-)D.y=2sin(gx一系)【分析】直接利用函数的图象的应用求出函数/(x)的关系式，进一步利用图象的变换的应用求出结果.【解答】解：根据函数的图象：A=2,T=2(-+-)=,1212所以3=2.当X=一工时，函数取得最小值，12故2x(-)+e=2k乃一,解得0=2%乃一。，keZ当4=0时，=.3故f(x)=2sin(2x-y),所以把f(x)=2sin(2x-工)的图象向右平移-个单位得到g(x)=2sin(2x-)=2sin(2x-),34236故选：C【跟踪训练2-3(2020春日照期末)已知函数/(x)=2SinQX+0)QO,*;T)的图象如图所示，则【分析】由三角函数的图象先求出周期，进而求出口的值为3,将(工，0)代入，注意在X=工处函数单调44递增，所以工