专题 锐角三角函数的应用 课后练习二及详解.docx

《专题 锐角三角函数的应用 课后练习二及详解.docx》由会员分享，可在线阅读，更多相关《专题 锐角三角函数的应用 课后练习二及详解.docx（6页珍藏版）》请在第壹文秘上搜索。

1、金题精讲题一：题面：在一次数学活动中，李明利用一根栓有小锤的细线和一个半圆形量角器制作了一个测角仪，去测量学校内一座假山的高度CO.如图，已知小明距假山的水平距离8。为12m,他的眼睛距地面的高度为1.6m,李明的视线经过量角器零刻度线OA和假山的最高点C,此时,铅垂线OE经过量角器的60。刻度线，则假山的高度为（）A.（43+l.6）mB.（123+1.6）mC.（42+1.6）mD.43m题二：题面：如图，小明想用所学的知识来测量湖心岛上的迎宾槐与岸上的凉亭间的距离，他先在湖岸上的凉亭A处测得湖心岛上的迎宾槐C处位于北偏东65。方向，然后，他从凉亭A处沿湖岸向正东方向走了100米到B处,测

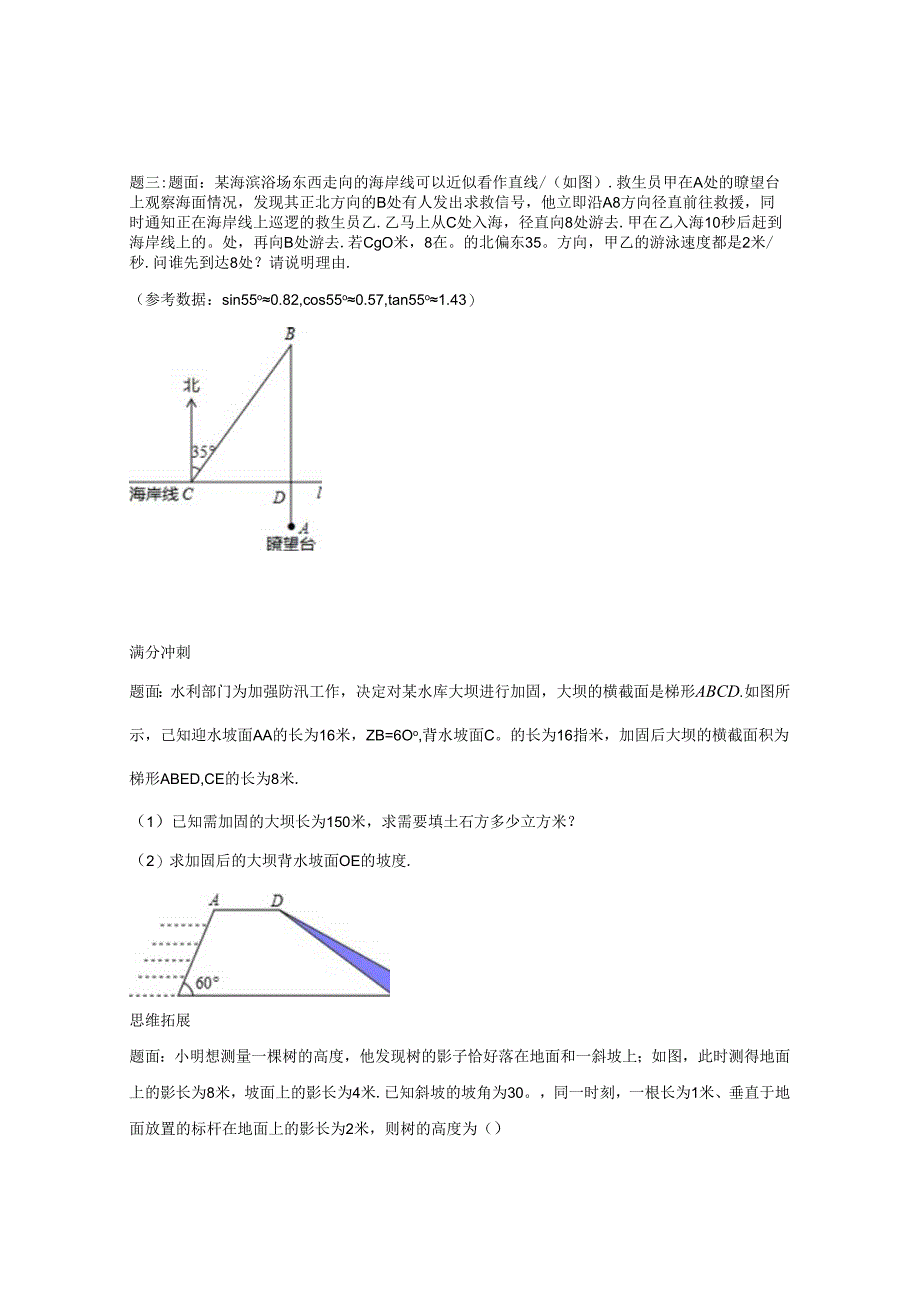
2、得湖心岛上的迎宾槐C处位于北偏东45。方向（点A、8、C在同一水平面上）.请你利用小明测得的相关数据，求湖心岛上的迎宾槐C处与湖岸上的凉亭A处之间的距离（结果精确到1米）.（参考数据：sin25o0.4226,cos25o0.9063,tan25o0.4663,sin65o0.9063，题三:题面：某海滨浴场东西走向的海岸线可以近似看作直线/（如图）.救生员甲在A处的瞭望台上观察海面情况，发现其正北方向的B处有人发出求救信号，他立即沿A8方向径直前往救援，同时通知正在海岸线上巡逻的救生员乙.乙马上从C处入海，径直向8处游去.甲在乙入海10秒后赶到海岸线上的。处，再向B处游去.若CgO米，8在。

3、的北偏东35。方向，甲乙的游泳速度都是2米/秒.问谁先到达8处？请说明理由.（参考数据：sin55o0.82,cos55o0.57,tan55o1.43）满分冲刺题面：水利部门为加强防汛工作，决定对某水库大坝进行加固，大坝的横截面是梯形ABCD.如图所示，己知迎水坡面AA的长为16米，ZB=6Oo,背水坡面C。的长为16指米，加固后大坝的横截面积为梯形ABED,CE的长为8米.（1）已知需加固的大坝长为150米，求需要填土石方多少立方米？（2）求加固后的大坝背水坡面OE的坡度.思维拓展题面：小明想测量一棵树的高度，他发现树的影子恰好落在地面和一斜坡上；如图，此时测得地面上的影长为8米，坡面上的

4、影长为4米.已知斜坡的坡角为30。，同一时刻，一根长为1米、垂直于地面放置的标杆在地面上的影长为2米，则树的高度为（）A.(6+3)XB.12米C.(4+2J)米D.10米课后练习详解金题精讲题一:答案:A.详解：如图，作AK_1.C。于点K,;BD=12米，李明的眼睛高A8=1.6米，ZAOE=GQo,。8=AK=I2米，AB=Ko=1.6米，NACK=60.VtanNACKAK=CKCK=AKtanNACK1212tan60。-W=43.，CD=CK+OK=4J+1.6=(4G+1.6)(米).故选A.题二：答案：207米.详解：如图，作Co_1.A8交AB的延长线于点。，则NBCZ)=4

5、5。，ZACD=65o.在RtZXACO和RtABCD中，设AC=f则AO=XSin65。，BO=CZ)=XCoS650.100+XCOS65。=XSin65.X=-207(米).sin65o-cos65，湖心岛上的迎宾槐C处与凉亭A处之间距离约为207米.答案：乙先到达B处.详解：由题意得N8CZ)=55。，ZBDC=90o.RD/tan/BCD-，.R11-rn.tjn/ArD=4Cxt1nSS0s7?CDCDrn(i/Rcn-Rr-CD40”CVJuZD-，BCQ1.-cos/.BCDcos5557O，一1.IC-2Q布卜、i-72一35I(M)，甲2NI/J，乙2；甲/乙答：乙先到达B

6、处.满分冲刺答案：(1)4800J立方米;走4.详解：(1)如图，分别过A、。作A/_1.BCDG1.BC,垂点分别为尸、G.AFT在RtZXAB尸中，AB=16米，NB=60。，sinZB=，AB/7AF=16-=83,BPDG=83.2又TCE=8,：.S2dce=1.cEDG=x8x8币-323.22又,需加固的大坝长为150米，需要填方：150x32J=48001.答：需要填土石方15Ox32J=48OG立方米.(2)在RtZXOGC中，DC=163,DG=83,GC=yDC2-DG2=24.GE=GC+CE=32.OE的坡度iDG83gF-2T答：加固后的大坝背水坡面OE的坡度为且.4思维拓展答案：A.详解：延长AC交BF延长线于。点，则NC30。.作CEj_8。于E,在RtC尸E中，NCFE=300,CF=A,CE=2,EF=4cos30o=23,在RIACEO中，CE=2,DE=4.同一时刻，一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,/.BD=BF+EF+ED=12+23.：adcesdab,且ce：de=i：2,/.在RtAABD中，AB=；8仄；(12+2G)=6+3.故选A.