数值计算 曲面(线)上法向量的散度是什么？.docx

《数值计算 曲面(线)上法向量的散度是什么？.docx》由会员分享，可在线阅读，更多相关《数值计算 曲面(线)上法向量的散度是什么？.docx（5页珍藏版）》请在第壹文秘上搜索。

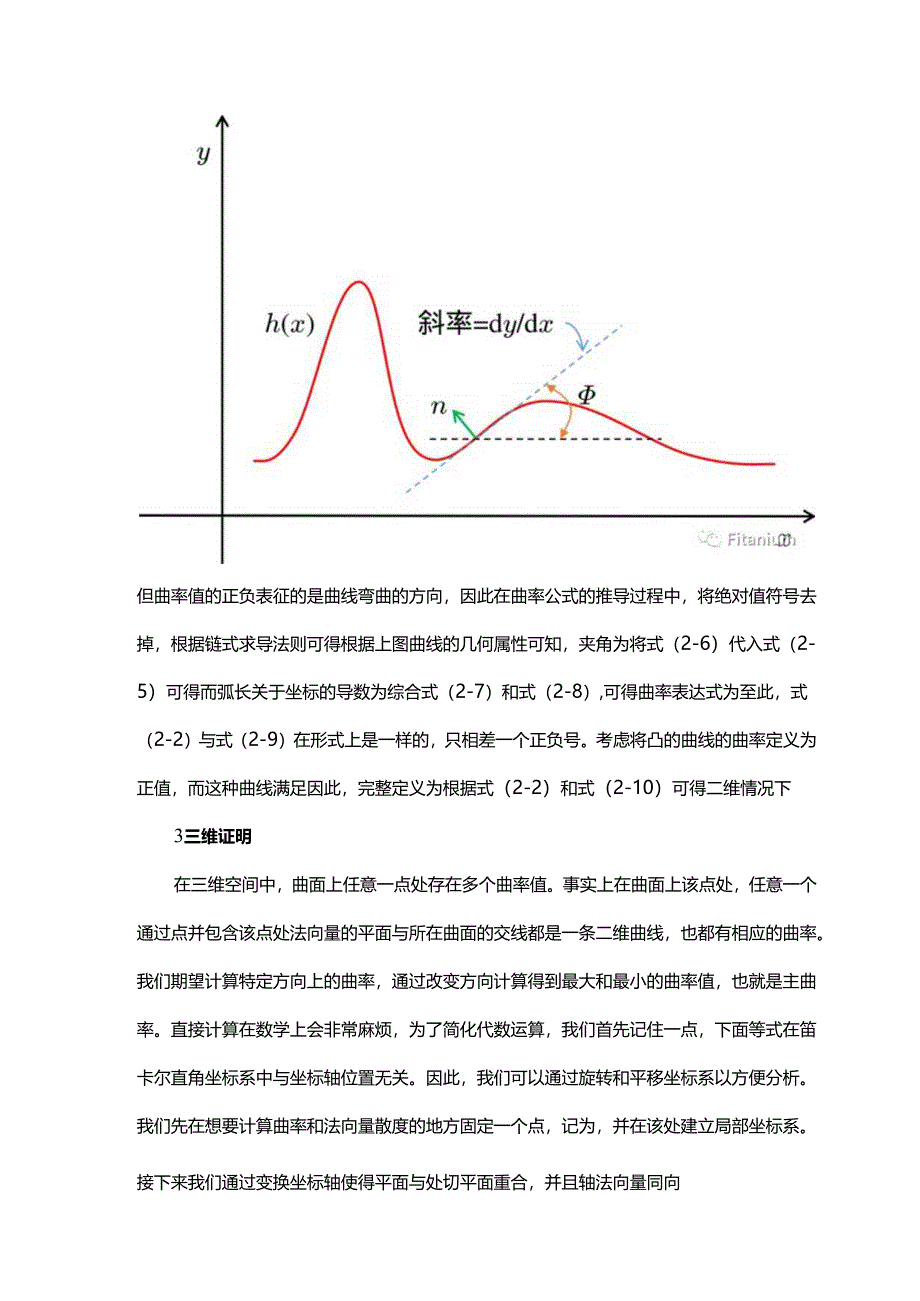
1、数值计算I曲面（线）上法向量的散度是什么？O写在前面在含有界面的流体流动模拟中，一般论文中常用的表面张力模型表达式为：其中，为表面张力系数，而在一些研究论文中通常将描述为曲率。那么它究竟是什么呢？在本文中，将详细推导曲面（或曲线）上法向量的散度。1问题说明在二维或三维空间中，定义曲线和曲面分别为和。假定这些函数具有连续二阶导数。在二维空间中，曲线上法向量的散度等于曲线的曲率（CUrVatUre）,也就是；在三维空间中，表面上法向量的散度等于主曲率（PrinCiPalCurvature）的和，主曲率的定义是包含法向量的平面与曲面交线的曲率的最大值和最小值，简单来说就是。2二维证明根据第一节的介绍

2、，我们可以定义曲线方程，则对应（外）法向量为对法向量求散度可得而多数微积分教科书中将曲线的曲率定义为正数其中，为曲线切向量与水平线之间的夹角，为曲线弧长。但曲率值的正负表征的是曲线弯曲的方向，因此在曲率公式的推导过程中，将绝对值符号去掉，根据链式求导法则可得根据上图曲线的几何属性可知，夹角为将式（2-6）代入式（2-5）可得而弧长关于坐标的导数为综合式（2-7）和式（2-8）,可得曲率表达式为至此，式（2-2）与式（2-9）在形式上是一样的，只相差一个正负号。考虑将凸的曲线的曲率定义为正值，而这种曲线满足因此，完整定义为根据式（2-2）和式（2-10）可得二维情况下3三维证明在三维空间中，曲面

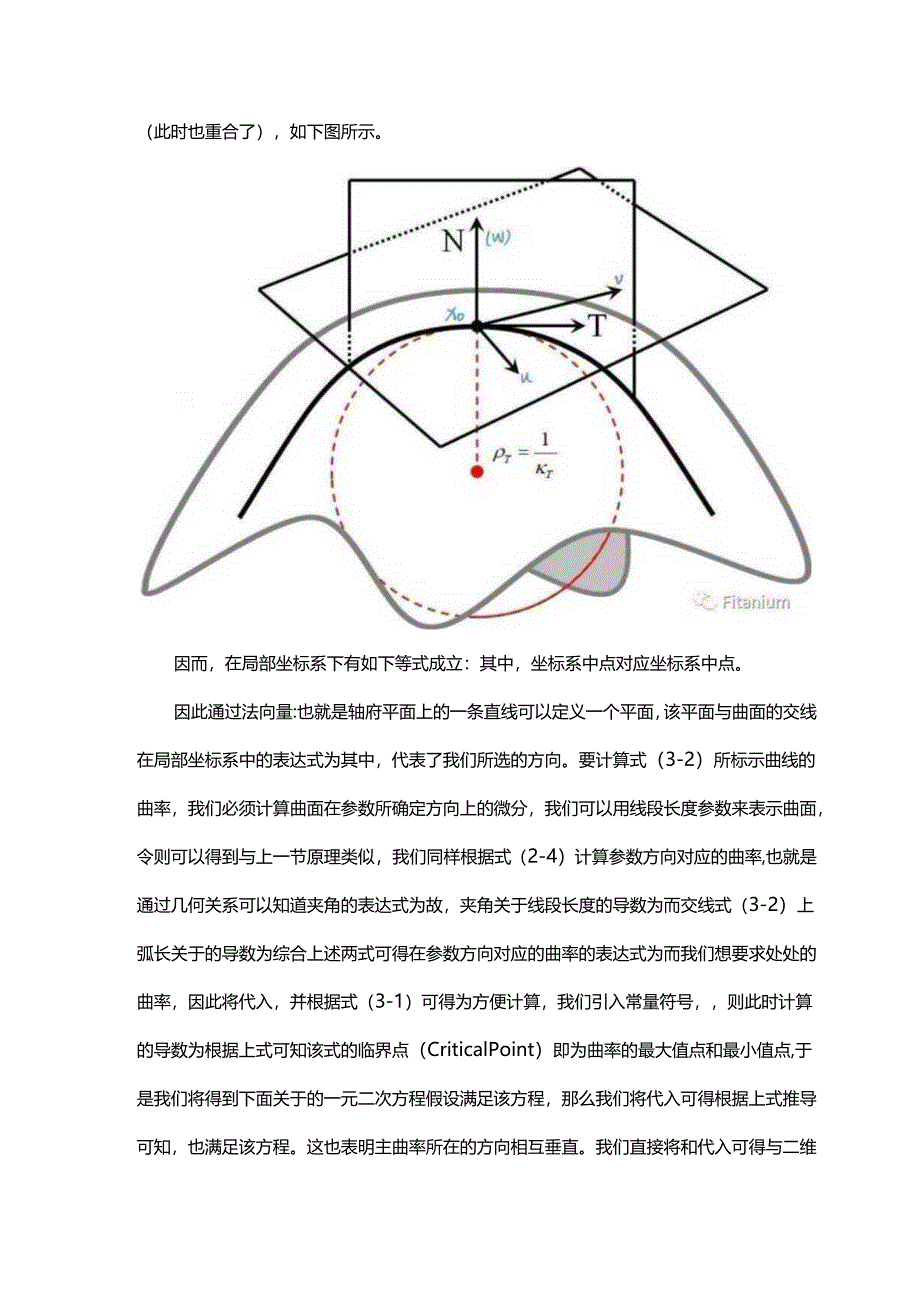
3、上任意一点处存在多个曲率值。事实上在曲面上该点处，任意一个通过点并包含该点处法向量的平面与所在曲面的交线都是一条二维曲线，也都有相应的曲率。我们期望计算特定方向上的曲率，通过改变方向计算得到最大和最小的曲率值，也就是主曲率。直接计算在数学上会非常麻烦，为了简化代数运算，我们首先记住一点，下面等式在笛卡尔直角坐标系中与坐标轴位置无关。因此，我们可以通过旋转和平移坐标系以方便分析。我们先在想要计算曲率和法向量散度的地方固定一个点，记为，并在该处建立局部坐标系。接下来我们通过变换坐标轴使得平面与处切平面重合，并且轴法向量同向（此时也重合了），如下图所示。因而，在局部坐标系下有如下等式成立：其中，坐标

4、系中点对应坐标系中点。因此通过法向量:也就是轴府平面上的一条直线可以定义一个平面，该平面与曲面的交线在局部坐标系中的表达式为其中，代表了我们所选的方向。要计算式（3-2）所标示曲线的曲率，我们必须计算曲面在参数所确定方向上的微分，我们可以用线段长度参数来表示曲面，令则可以得到与上一节原理类似，我们同样根据式（2-4）计算参数方向对应的曲率,也就是通过几何关系可以知道夹角的表达式为故，夹角关于线段长度的导数为而交线式（3-2）上弧长关于的导数为综合上述两式可得在参数方向对应的曲率的表达式为而我们想要求处处的曲率，因此将代入，并根据式（3-1）可得为方便计算，我们引入常量符号，则此时计算的导数为根

5、据上式可知该式的临界点（CriticalPoint）即为曲率的最大值点和最小值点,于是我们将得到下面关于的一元二次方程假设满足该方程，那么我们将代入可得根据上式推导可知，也满足该方程。这也表明主曲率所在的方向相互垂直。我们直接将和代入可得与二维情况相同，我们也需要选择一个符号来表示凸的曲面的正曲率，与二维同理可得现在，我们在局部坐标系下计算面法向量的散度为因此，根据式（3-1）所述性质，在处有根据式（3-8）式（3-9）可得三维情况下证毕。参考费料AProofthattheDivergenceofaSurfaceNormalIsEqualtothesumofthePrincipalCurvat

6、ureshttps:/willson.cm./Research/Sub_Files/Surface_Phenomena/Spring%202000/surface_normal_proof.pdf#:-:text=Then%20in%20t%20w%20o%20dimensions%2C%20the%20divzto%20surface%20is%20equal%20sum%20principal%20curv%20atures.NicholasM.Patrikalakis,TakashiMaekawazWonjoonCho.ShapeInterrogationforComputerAided

7、DesignandManufacturing:Principalnormalandcurvaturehttpsweb.hyperbookPatrikalakis-Maekawa-Chonode23.htmlNicholasM.Patrikalakis,TakashiMaekawazWonjoonCho.ShapeInterrogationforComputerAidedDesignandManufacturing:Curvatureandcurvaturevectorhttpsweb.hyperbookPatrikalakis-Maekawa-Chonodell9.html#sec:dgint_trans_curv请问如何根据二阶导判断函数凹凸性？Relationbetweendivergenceofunitnormalandradiusofcurvaturehttpsphysics.questions698035relation-between-divergence-of-unit-normal-and-radius-of-curvature